1.概要

• 仕事で外国人とやり取りする時に数学用語はよく使う
• その時に、パッと英語で数学用語がでないと困る
• また、LatexはMarkdownで記述する時によく使う
• そこで、Latexと英語とRでの数学用語の基本的なメモを残す

NOTE:

• 便宜上形式的にLaTeXをLatexと表記する

2.LaTex

2.1.論理学系用語

これで基本的な用語は充足しているだろう。

2.2.変数（variable）

$$x = 10$$

変数の修飾

• 全ての変数（all variable）
  • $n$の下付き文字で定義時に表す

$$X = X_1, X_2, \cdots ,X_n$$

• 各変数（every variable）
  • n項演算子と$i$の下付き文字で表す

$$S = \sum_{i=0}^{n}X_i$$

• 任意の変数（any variable）
  • n項演算子なしの場合は、$i$の下付き文字で表す

$$E(X_i) = \mu$$

アクセント

• 循環小数

$$\dot{a} = 0.9999$$

• 推定値

$$\hat{x} = 12$$

• 平均

$$\bar{x} = 12$$

• 複素共役と補集合
  • （エルミート共役と紛らわしいので、アスタリスクではなくバーで表す）

$$\bar{z}$$

• 随伴行列（エルミート共役）
  • 随伴行列はアスタリスク

$$A^{*}$$

R

1

x <- 12

ドットは単なる名前（dataオブジェクととかではない）

1
2

data.train <- xxx
data.test <- xxxxx

型の意味

型の例

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

> x <- as.Date('2010-01-01')
> x
[1] "2010-01-01"
> class(x)
[1] "Date"
> typeof(x)
[1] "double"
> mode(x)
[1] "numeric"
> unclass(x)
[1] 14610

2.3.分数（Fraction）

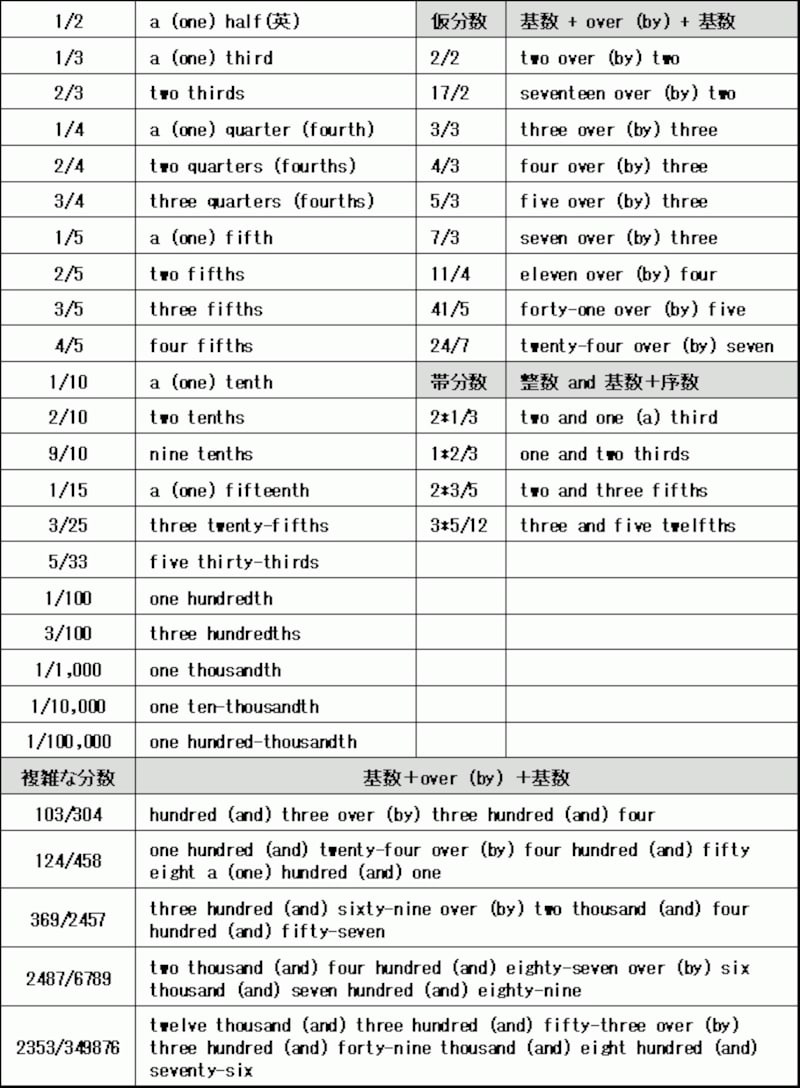
英語での分数の読み方のルールは次になる。

• 分母は「denominator, denom.」
• 分子は「numerator, numer.」
• 分数を「分子 -> 分母」の順で読む
  • 分子は基数（cardinal numbers）を使う
  • 分母は序数（ordinary numbers）を使う
    • 序数は次の2つの意味がある
      • Third: 3番目
      • Third: 1/3
• ただし以下に注意
  • 1/1の時
    • one whole
    • one over one
  • 分子が0の場合
    • zero thirds（0/3）
  • 分子が1
    • 分子はaかoneで、分母は単数形
      • 分母が2の時
        • one half (1/2)
        • a half (1/2)
        • one second (1秒) <= 間違い
        • half a second （0.5秒）<= 間違い
      • 分母が3の時
        • one third (1/3)
      • 分母が4の時
        • a quarter
        • one fourth <= よりフォーマル
  • 分子が1より大きい
    • 分母は複数形
      • 分母が2の時
        • two halves（2/2）
        • two seconds (2秒) <= 2秒なので注意
      • 分母が3の時
        • two thirds（2/3）
      • 分母が4の時
        • two quarters（2/4）
        • two fourths（2/4） <= これは一般的ではない
      • 分母が5, 6の時
        • two fifths（2/5）
        • two sixths（2/6）
        • three twelfths（3/12）
      • 分母が巨大な時
        • one hundredth (1/100) <= これでもOK
        • one over one hundred (1/100) <= こっちが一般的
  • 分子や分母が少数の時は
    • one point four fifths
    • one point five over three
    • one point five divided by three
  • 帯分数の場合はandで繋げる
    • three and a half (3 + 1/2)
    • three times one-half （3 x 1/2）
  • 分母が分子より大きいとき
    • 5 out of 10
• その他
  • tenth of a millimeter（ミリメートルの十分の一）

2.4.記号（symbol）

2.5.集合（set）

• 集合は大文字
• 元（要素）は小文字

$$X = \{x_1, x_2, x_3\}$$

特徴づけ（characterize）

• 性質P（property）が対象Xを特徴づける

$$X = \{x | P(X) \}$$

• もしくは条件

$$X = \{x | x \in \mathbb{R} \}$$

条件付き確率（$P(X|C)$）の場合は括弧、特徴付けは波括弧の中でパイプをつかう

集合の関係

2.6.数の集合（Set of numbers）

例

$$3\in\mathbb{N} \\ 3.14\notin\mathbb{Z} \\ \mathbb{Q}\subset\mathbb{R} \\$$

2.7.関数（function）

関数

$$y = f(x) = 2x$$

関数の引数が複数の場合。
コロンの場合は、複数引数を使う。

$$f(x, x_2) = x + x_2$$

セミコロンの場合は、セミコロンの前は変数、セミコロンの後はパラメータとなる。

$$f(x; a,b) = (x^a)e^{(-x/b)}$$

セミコロンの意味:

• $f(x; a, b)$ はパラメータ$a, b$によって特徴付けられる、$x$変数の関数$f$みたいなイメージ
• つまり、$a,b$は係数としての性格が強く、$a,b$を固定して$x$の関数と見なすことが多い

ベクトル関数

$$\mathbf{y} = \mathbf{a}(x)$$

写像

$$f: \mathbb{R} \mapsto \mathbb{R}$$

場合分け

$$y = \begin{cases} 1 & (n=0) \\ x^{n-1} & (otherwise) \end{cases}$$

R

1
2
3
4
5
6
7
8
9

> f <- function(a,b=2){
  return(a * b)
  # a*b #←return省略も可能
}

> f(2)
[1] 4
> f(b=3,a=2)
[1] 6

2.8.集計関数（aggregate function）

総乗

$$f(x) = \sum_{i=0}^n x_i$$

総乗

$$f(x) = \prod_{i=0}^n x_i$$

集合を使った場合

$$f(x) = \sum_{i\in N} x_i$$

R

• max / min / which.max / which.min 最大値/ 最小値/ 最大値のある場所 / 最小値のある場所
• unique 重複除去
• sum / mean / median / var 合計 / 平均値 / 中央値 / 不偏分散

2.9.三角関数（trigonometric function）

R

1
2
3
4
5
6

> cos(0)
[1] 1
> cos(pi/2)
[1] 6.123234e-17
> cos(pi)
[1] -1

2.10.ギリシャ文字（greek letters）

変数

2.11.数列（sequence）

$$x = \{1, 2, 3\}$$

2.12.指数（exponential）

指数関数のグラフ。

• 定義域（domain）
  • (-∞,∞)
• 値域（range）
  • (0,∞)

R

1
2
3
4
5
6

> exp(1)
[1] 2.718282
> exp(0)
[1] 1
> exp(2)
[1] 7.389056

ネイピア数はexp(1)で表現する

1
2
3
4

> exp(1)^2
[1] 7.389056
> 10^2
[1] 100

2.13.級数（series）

$$s = \sum_{i=0}^{n}x_i$$

R

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

> seq(1,10,length=5)  #1~10を5分割で
[1]  1.00  3.25  5.50  7.75 10.00
> seq(1,10,by=2) #1から2ずつやして10まで
[1] 1 3 5 7 9

> rep(1:3,times=2) #(1,2,3)を2回
[1] 1 2 3 1 2 3
> rep(1:3,length=5) #(1,2,3)を5個になるまで繰り返す
[1] 1 2 3 1 2
> seq(as.Date("2016-01-01"),as.Date("2016-01-05"),by="day")
[1] "2016-01-01" "2016-01-02" "2016-01-03" "2016-01-04"
[5] "2016-01-05"

2.14.区間（interval）

開区間

$$x = (1, 2, 3)$$

閉区間

$$x = [1, 2, 3]$$

2.15.ベクトル（vector）

$$\vec{a} = \mathbf{a} = (1, 2)^T$$

R

1
2
3
4
5

> vec <- c(1,2,1,2,3,4,1,2,3)
> vec
[1] 1 2 1 2 3 4 1 2 3
> vec[3]
[1] 1

2.16.累乗/冪乗（power）

表記

累乗と冪乗の違い

2.17.対数（Logarithm）

対数関数のグラフ。

• 定義（domain）
  • (0,∞)
• 値域（range）
  • (-∞,∞)

常用対数と自然対数

• 対数は、底（base）$a$と真数（antilogarithm）$x$を使って $log_a x$ と書くのが正式な表記。

R

ちなみに、Rにはネイピア数の定数はないので、exp(1)を使う必要がある

1
2
3
4
5
6
7
8
9

> e <- exp(1)
> e
[1] 2.718282
> log(e)
[1] 1
> log(1)
0
> log2(8)
[1] 3

2.18.累乗根（root）

• 平方根（Square Root）
  • The square root of x

$$\sqrt{x}$$

• 立方根（Cube Root)
  • The cube root of x

$$\sqrt[3]{x}$$

• N-th根
• The n-th root of n

$$\sqrt[n]{x}$$

2.19.行列（matrix）

集合は小文字、行列は太字。

$$\mathbf{A} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$$

R

1
2
3
4
5

> x <- matrix(1:8, ncol=4)
> x
     [,1] [,2] [,3] [,4]
[1,]    1    3    5    7
[2,]    2    4    6    8

データフレーム (行列にヘッダをつけたもの)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

> sex    <- c("F","F","M","M","M")
> height <- c(158,162,177,173,166)
> weight <- c(51,55,72,57,64)
> x    <- data.frame(SEX=sex, HEIGHT=height, WEIGHT=weight)
> x
  SEX HEIGHT WEIGHT
1   F    158     51
2   F    162     55
3   M    177     72
4   M    173     57
5   M    166     64
> x$SEX
[1] "F" "F" "M" "M" "M"

2.20.極限（limit）

2.21.微分（derivative）

2.22.微分・勾配記号（derivative symbol）

1次微分

$$\dot x = x^{\prime} = dx/dt=\frac{d x(t)}{d t}=\frac{d}{d t}\left(x(t)\right),$$

2次微分

$$\ddot x = x^{\prime \prime} = d^{2}x/dt^{2}=\frac{d^{2} x(t)}{d t^{2}}=\frac{d^{2}}{d t^{2}}\left(x(t)\right),$$

偏微分

$$\frac{\partial f(x,y)}{\partial x} =\partial_{x}f(x,y)=f_{x}(x,y),$$

2.23.積分（Integral）

$$\int f(x)dx, \ g(x)=\int^{x} f(x')dx', \ \int_{\alpha}^{\beta} f(x)dx.$$

面積分（surface integral）

$$\int\int_{S} f(x,y) , \mathrm{d}x , \mathrm{d}y$$

線積分（line integral）

$$\quad \oint_{C} f(z){\rm d}z$$

2.24.組合せ（combination）

• 組み合わせ（combination）
• 順列（permutation）
• 斉次積（Homogeneous product）

2.25.階乗（factorial）

$$5! = 5 \times 4 \times 3 \times 2 \times 1$$

3.まとめ

• 数字は民主的であり、証明は理路整然とした論理を求める
• 外国人にも伝わりやすいし、日常会話でも序数で条件を挙げると納得されやすい
• 故に正しく使って効率良くコミュニケーションを取るのが大事

4.参考文献

• Mode, Class and Type of R objects - Cross Validated
• What is the difference between mode and class in R? - Stack Overflow
• 記号の定義
• 小数・分数の英語表現！帯分数の英語で表す方法も [ビジネス英会話] All About