目次
概要
- 数年間に渡って画像処理の仕事をしてきた時に残っていた古典的画像処理周りのメモ
- 特に、2012年以前のCNNを代表とするDNN系の手法、最近のViT系の手法は別の記事にまとめる
- 画像処理でよく使うlibraryはnumpy, opencv, scikit-image, matplotlib, jupyterlab, pytorch, dlib, imageprayなどなど
- 個人的に使うOpenCVのスニペットも残す
知識メモ
基本
画像の種類
大きく分けて2種類ある。
- ベクター画像
- ベクター画像は、線や曲線といった図形集合の重ね合わせをデータとして保持した形式
- e.g. svg
- ラスター画像
- ラスター画像はピクセル(画素ともいう)と呼ばれる色の数値を格子状に並べたデータを保持した形式
- e.g. png, jpg
画像の圧縮方式の違い
- PNGは可逆圧縮だが、JPGは非可逆圧縮
- つまり、JPGはデータの圧縮の際にデータを削除するので小さな線分やオブジェクトが劣化する可能性がある
- 一般的には、PNGを使うのを推奨
- ただし、ベクトル化した場合はSVGを推奨
色空間
- 色空間(カラースペース)とは、色を数値に変換するシステムのこと
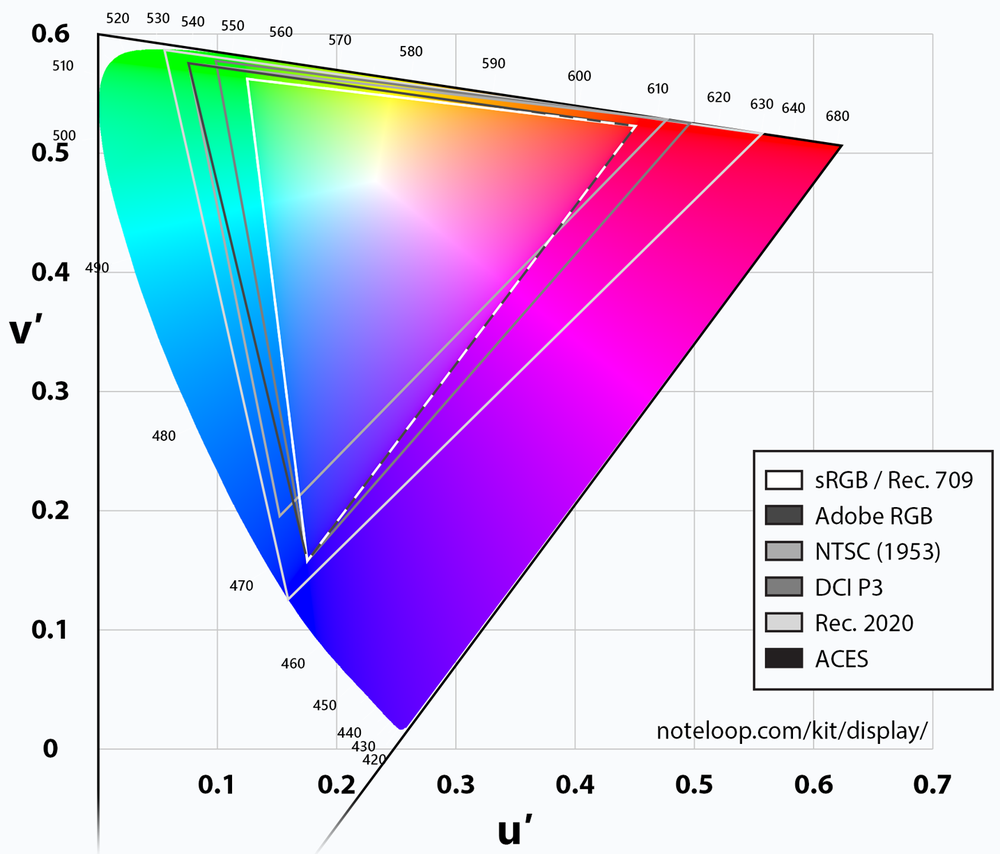
レンダリングするメディアタイプによって、色域は異なるので注意。

OpenCVでは次の型だが、おおむねCV_8U=np.uint8を使う。
| 型 | 範囲 |
|---|---|
| CV_8U | 0 - 255 |
| CV_16U | 0 - 65535 |
| CV_32F | 0 - 1 |
また、色変換によって分類の一助になる可能性もあるため、分析をする前に先に確認するのも良い。
| |
入力画像

出力画像
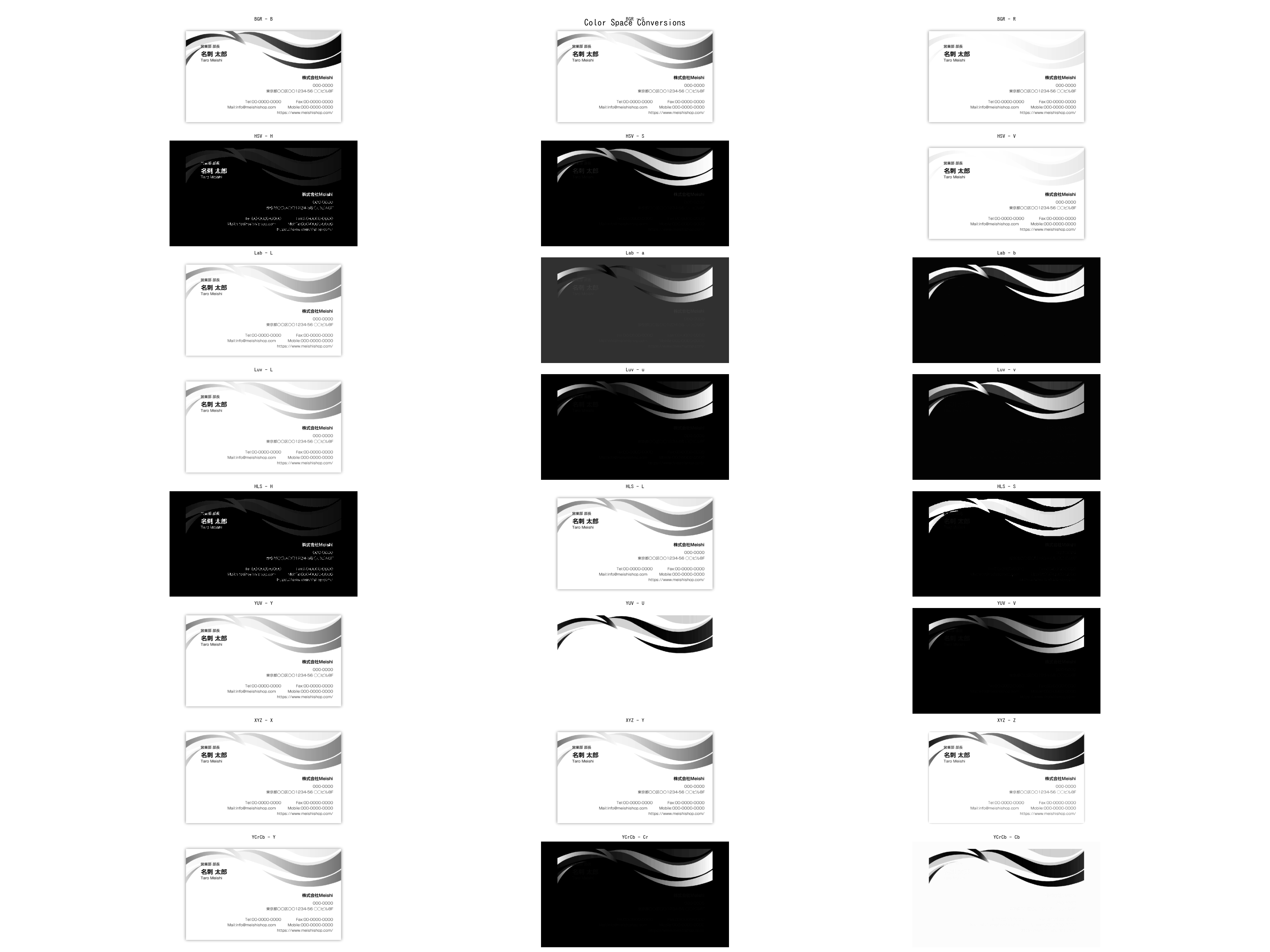
カラースペースの特徴は以下になる。
| カラースペース | 変換コード | チャネル | 特徴 |
|---|---|---|---|
| BGR | cv.COLOR_BGR2BGRA | B, G, R | 青、緑、赤の基本的なRGBカラースペース。一般的なカメラで使用される形式。 |
| BGRA | cv.COLOR_BGR2BGRA | B, G, R, A | BGRカラースペースにアルファチャネルを追加。透過性を持つ。 |
| HSV | cv.COLOR_BGR2HSV | H, S, V | 色相、彩度、明度のカラースペース。色を直感的に理解しやすい。 |
| Lab | cv.COLOR_BGR2Lab | L, a, b | 光度(L)と2つの色成分(a、b)のカラースペース。人間の視覚に近い。 |
| Luv | cv.COLOR_BGR2Luv | L, u, v | 光度(L)と2つの色成分(u、v)のカラースペース。CIE 1976 L*u*v* 標準。 |
| HLS | cv.COLOR_BGR2HLS | H, L, S | 色相、光度、彩度のカラースペース。HSVと似ているが、光度が異なる。 |
| YUV | cv.COLOR_BGR2YUV | Y, U, V | 輝度(Y)と2つの色成分(U、V)のカラースペース。ビデオ圧縮に使用される。 |
| XYZ | cv.COLOR_BGR2XYZ | X, Y, Z | CIE 1931標準色度図のカラースペース。標準色度としてよく使用される。 |
| YCrCb | cv.COLOR_BGR2YCrCb | Y, Cr, Cb | 輝度(Y)と2つの色成分(Cr、Cb)のカラースペース。映像処理に使用される。 |
画像の状態
画像が現実の写像になっていない時に使われる用語。
| 英語 | 日本語 | 対義語 |
|---|---|---|
| noised | ノイズのある | clean |
| rotated | 回転した | upright |
| distorted | 歪んだ(レンズの歪みなどの、不規則な変形) | undistorted |
| skewd | 傾斜した(透視的効果などによる特定の方向への変形) | Aligned(整列した)など |
| unclear | アンクリア | clear |
| blurred | ぼやけた | sharp |
| superimposed | スーパーインポーズされた(重ねられた) | isolated |
他にも色々あるが、imgaugのtoolのgifが分かりやすい。
aleju/imgaug: Image augmentation for machine learning experiments.
座標系
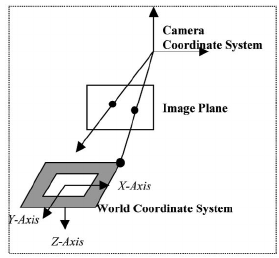
代表的な座標系
いくつかあるが、次などが頻出する
- ワールド座標系
- カメラ座標系
- ピクセル座標系
- topleftがx, y = (0, 0)
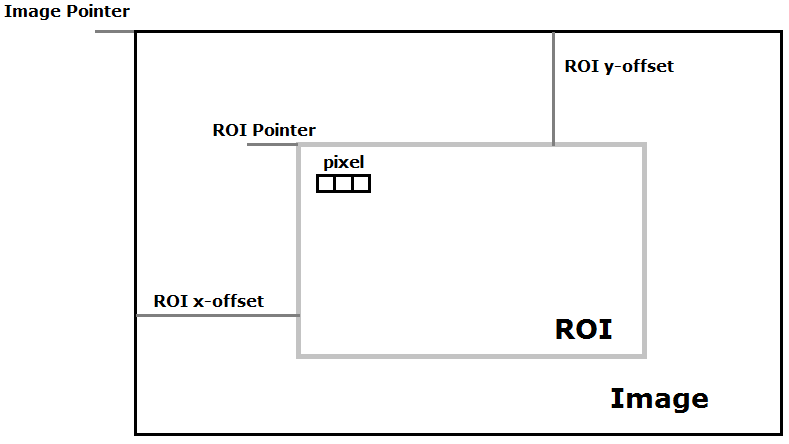
絶対座標・相対座標
2次元の画像処理では、ピクセル座標が絶対座標で、ROI内の座標が相対座標。
紙に対する処理
アンチエイリアス
「アンチエイリアス」は描いた線のフチを僅かにボカして、なめらかな線に見えるよう変換するといった、ペン・図形・選択範囲などあらゆる描画ツールに付加できる機能。
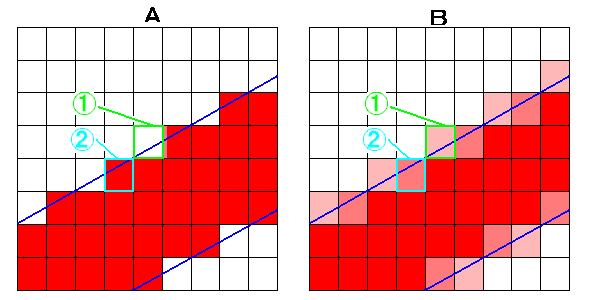
deskew
スキャンしたデータの傾きなどを修正する事。
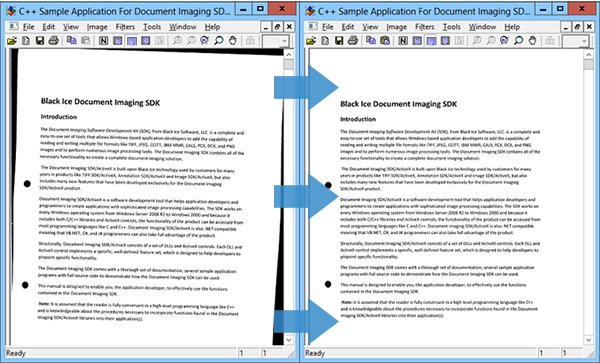
紙からデータを抜き出す鉄板パターン
特に紙の場合は色が単一でデータがスパースなので、画像処理がやりやすい特徴がある。
- グレースケール
- 白黒をインバート
- 文字が白に、背景が黒に
- コンター(contour)をとる
- 文字や図などの輪郭をとる
- 図形化する
ビット演算子で画像を合算処理する方法。
- よく使われるのが、白黒でのAND
- ある2つの処理が合った時に、完全に両方のオペランドで黒(0)じゃないときは、白にするというやり方
- つまり、2つの処理の両方で通った時のみ、表示するというやり方
| |
カメラ
キャリブレーション
- カメラが物理的にどう見ているかを理解するために、カメラの内部および外部のパラメータを特定するプロセス
- カメラのレンズの歪みを表現するパラメータや、カメラのワールド座標系での位置姿勢を推定できる
内部パラメータ・外部パラメータ
- 内部パラメータ
- レンズ歪みの具合などを表すパラメータ
- 外部パラメータ
- カメラの位置、向き、回転など、カメラが世界に対してどう配置されているかのパラメータ
ROI系
ROIとは
- ROI: Region of Interest
- 分かりやすく言うと、興味があるところ
- Subpixelとも言ったりもする
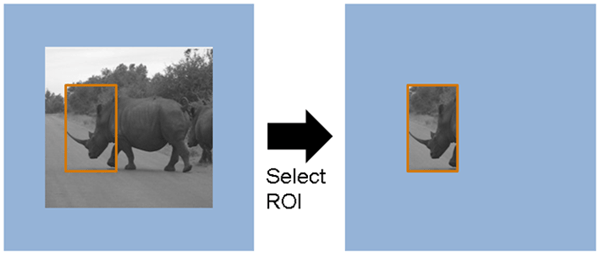
Saliency Map(顕著性マップ)
Saliency Mapとは、ある画像を人が見ると、視線はどこに向くか?をピクセル単位で考えたもの。

図:Saliency Mapの例。
- 左上:画像
- 右上:実測した視点を赤いXで示したもの
- 左下:Saliency Map
- 右下:Saliency Mapをカラーにして画像に重ねたもの
Segmentation
セグメンテーションとは
Image segmentation is the process of partitioning a digital image into multiple segments by grouping together pixel regions with some predefined characteristics. Each of the pixels in a region is similar with respect to some property, such as color, intensity, location, or texture. It is one of the most important image processing tools because it helps us to extract the objects from the image for further analysis. Moreover, the accuracy of the segmentation step determines success and failure in further image analysis.
セグメンテーションの4つの特徴
重要なの4つの特徴
- color: 色
- intensity: 強度(いわゆるコントラスト)
- location: 場所
- texture: パターン
セグメンテーションの種類
やりかたは、discontinuity か similarityの強さに応じて2つに大分される。
- The discontinuity approach splits an image according to sudden changes in intensities (edges).
- The similarity approach splits an image based on similar regions according to predefined criteria
テクニックは次のような感じ。
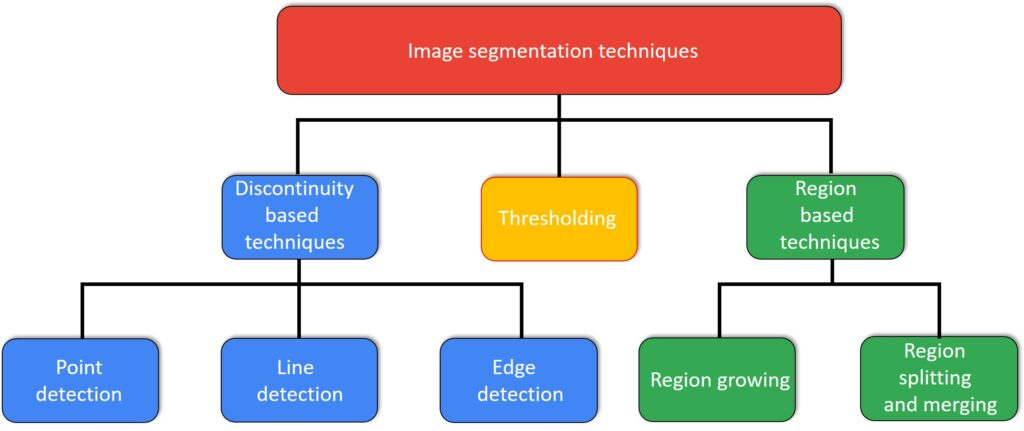
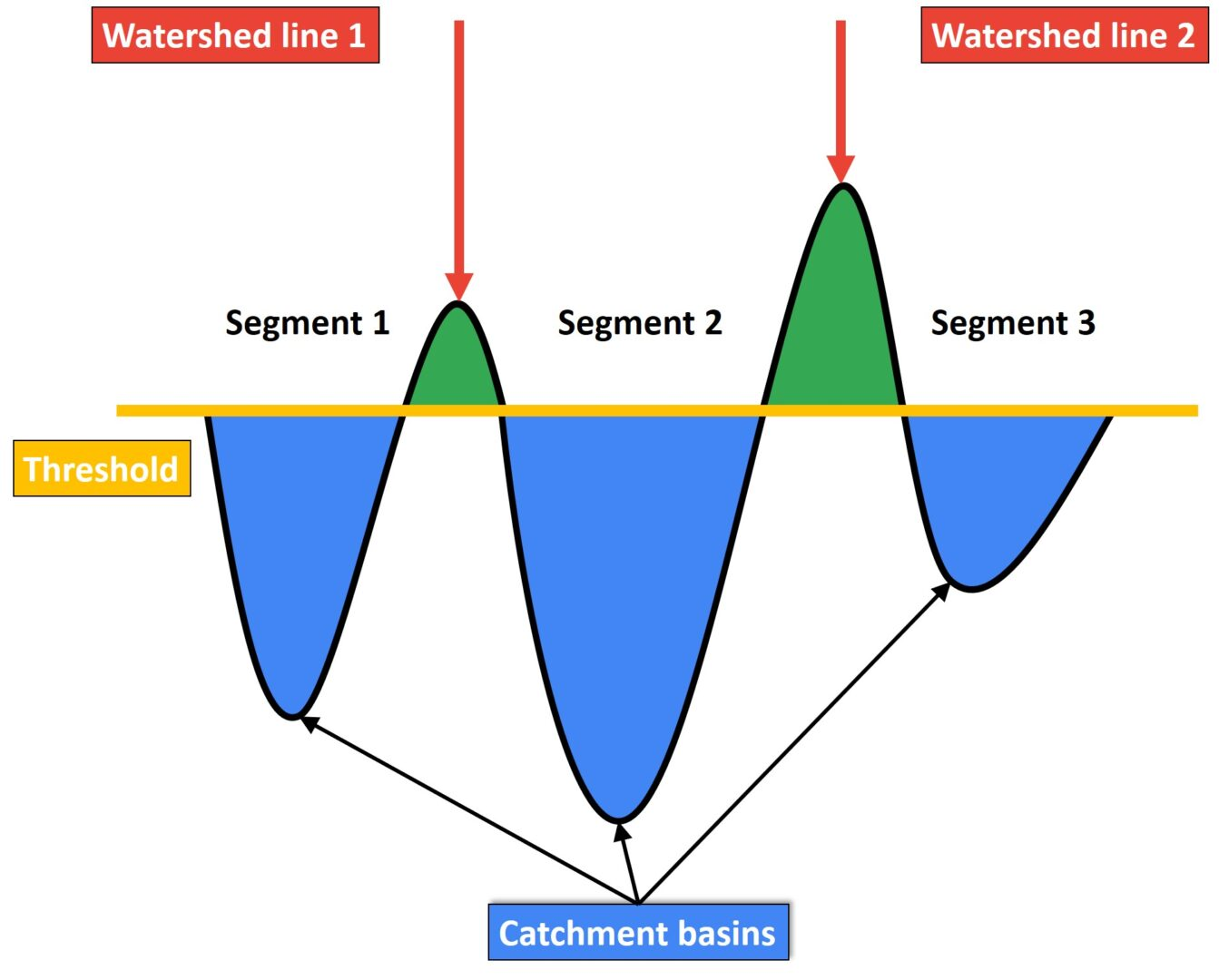
Watershed(分水界)とは
OpenCVでのWatershed algorithmについて。 イメージはダム。ダムの水を堤防の限界まで埋めるように処理が走る。
ノイズ除去系
デノイズ
cv2.fastNlMeansDenoisingを使う

Blurryな画像をClearにする方法
目的に応じて使い分ける必要がある。
- binarizationで分ける
- binarizationできるならそれでOK
- blurでノイズを消す
- GaussianBlurなどをかけてnoiseを消す
- 傾きが強いKernelを適用する (Sharpen Filter)
1 2sharpen_filter = np.array([[0, -1, 0], [-1, 5, -1], [0, -1, 0]]) sharped_img = cv2.filter2D(image, -1, sharpen_filter) - Unsharp masking
画像の微細構造(高周波成分)を強調するために使われる画像処理の技法。原画像をピンぼけ状態にぼかした画像(アンシャープマスク)を原画像から差し引くことで、微細構造が強調される。写真の場合は、アンシャープマスクを原画像とネガポジ反転させて重ねて焼き付ける。マスクのピンぼけ状態の度合いを変えることで、強調される微細構造の細かさを変化させることができる。
- scikit image のapiをつかう
- モルフォロジー変換を使う
- ガウシアンフィルタ
- 画像を平滑化するのに使う

カーネル系
ConvとPoolの違い
DNNではおおむね次の2つのフィルターをかけるが、数学的には次の違いになる。
- Conv:
- 特徴マッチの為の処理
- invariant function
- Pool:
- 位置情報の為の処理
- variant function
代表的なカーネル
代表的なのは下。

- Mexican hat or Laplacian filter.
- エッジ検出や特徴抽出、画像の特定部分を強調するために使われる

- バイラテラルフィルタ(Bilateral filter)
- 単純に注目画素の周りにある画素値を平均するのではなく、注目画素の近くにあるものをより重視して反映させようというのが重み付き平均化
- じゃあその重みの振り分けをどうするかというときに、正規分布に従って振ればいいんじゃないというのがガウシアンフィルタ

- ノンローカルミーンフィルタ(Non-local Means Filter)
- バイラテラルフィルタは注目画素の画素値と周辺画素の画素値の差に応じた重みをつけたけど、ノンローカルミーンフィルタはテンプレートマッチングのように周辺画素を含めた領域が、注目画素の周辺領域とどれくらい似通っているかによって重みを決定するフィルター

- ガボールフィルタ(Gabor filter)
- ガボール関数はガウス関数と正弦・余弦関数から構成されている関数
- 任意の周波数成分を抽出するフィルタリング機能を持つ
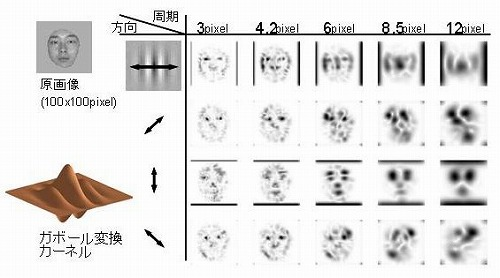
- CNNのフィルタ
- CNNのConv、Poolなどのカーネルを古典的なアルゴと併用してを使う事もできる
- ImageNetなどで学習済みのCNNモデルのDNNを使ってベクトルを産出しできる
- それをPCAなどにかける事で、少数画像で教師あり学習(クラスタリング)をする事も可能
白と黒の意味
- CVだと、白=1、黒=0となる
- 0は谷/海となり、1は峰/丘となる
- 処理でも残したい所=白、消したい所=黒とする
- グレースケールのときは、黒=0、白=255
- 0は何かけても0なので、掛け算の処理をしても無効化もできる
- さらに、ビット変換の際にも役立つ
- 白黒反転したいときは、インバートする
白い所(180 ~ 255)を消す例。
| |
ベクトル化
ベクトル化(スケルトン化)
次のように情報を縮尺する事。
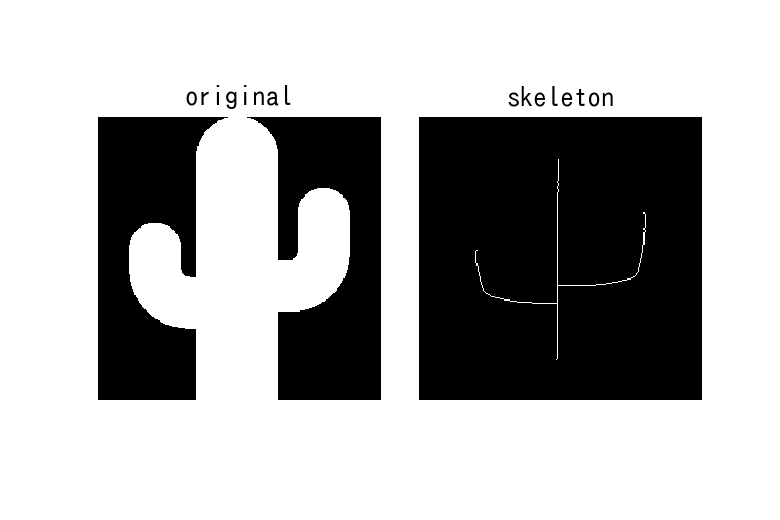
グラフ化
- この場合は、赤い点がnode
- そして、緑の線がedgeとなる
- edgeは2つのnode(start, end)をもつ
- これらの2つの点を結ぶedgeをベクトル化(曲線化)する方法がベジェ曲線
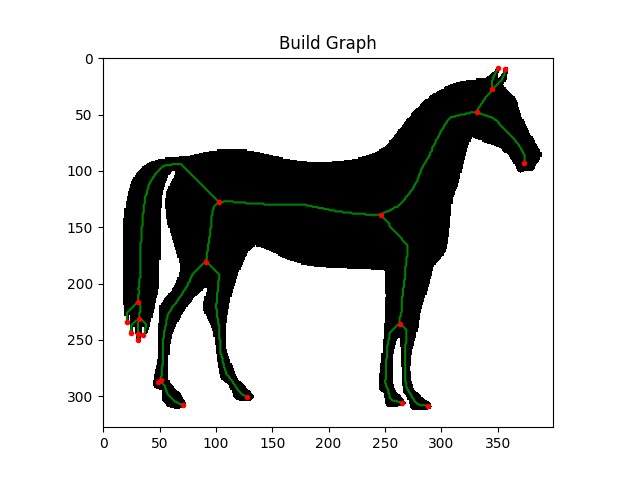
ベジェ曲線
ベジェ曲線(Bezier Curve)とは、複雑な凹凸を持つ曲線でも、制御点の座標と関数により指定した二点間を結ぶ滑らかな曲線を表現できる手法。
凸包(convex hull)
凸包とは
凸包(convex hull)とは, 与えられた点をすべて包含する最小の凸多角形(凸多面体)のこと。
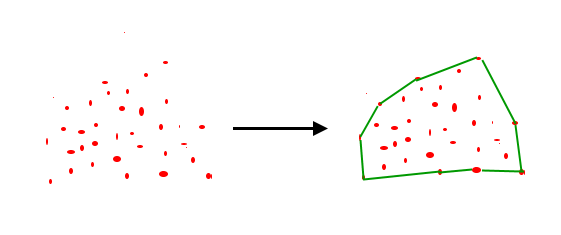
凸性の欠陥とは?
簡単に言うと、凸性の欠陥とは、手のひらのくぼみと赤線の凸包の間のこと。
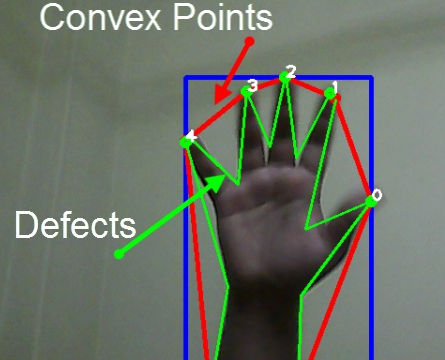
凸製の欠陥の例
| |
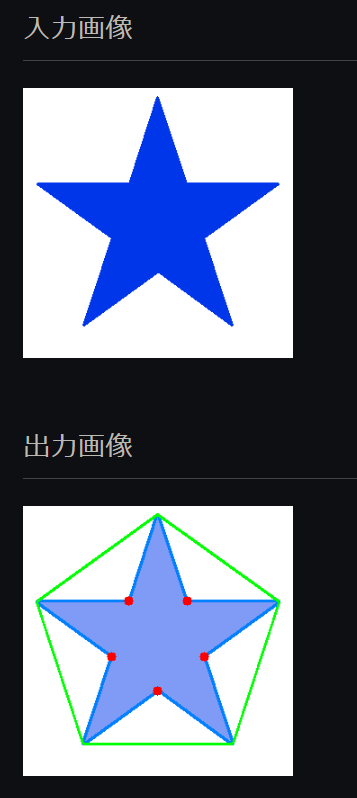
検出
線分検出
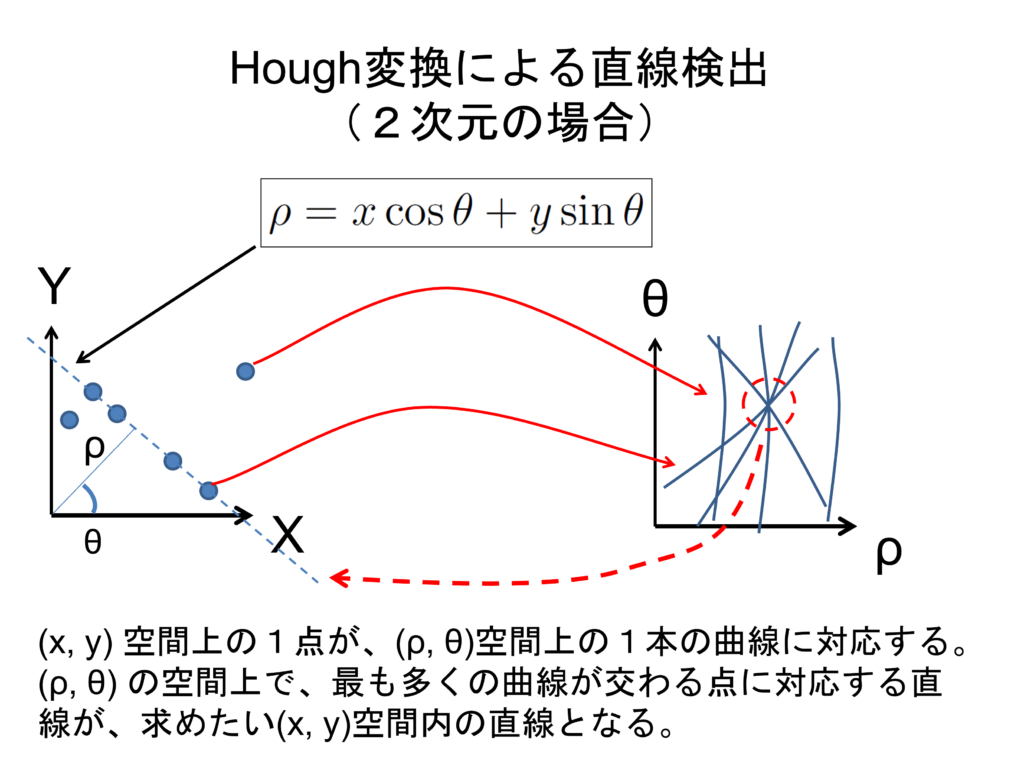
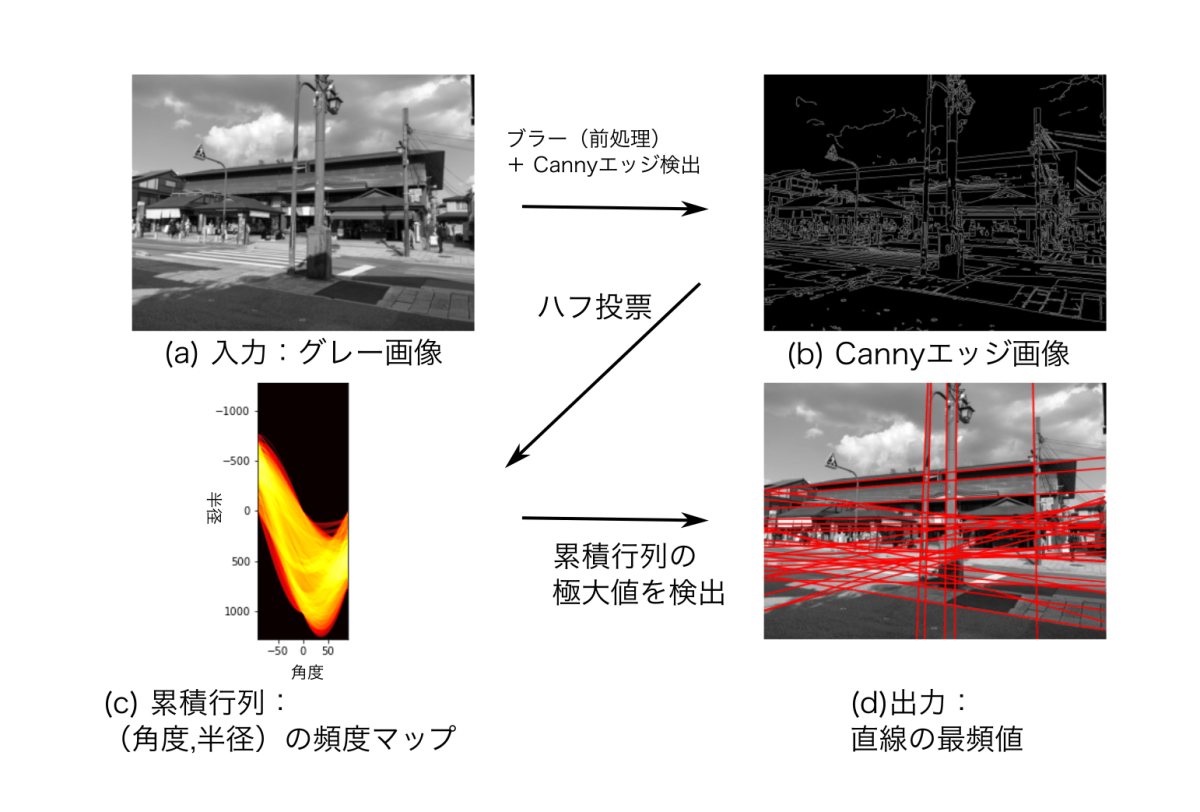
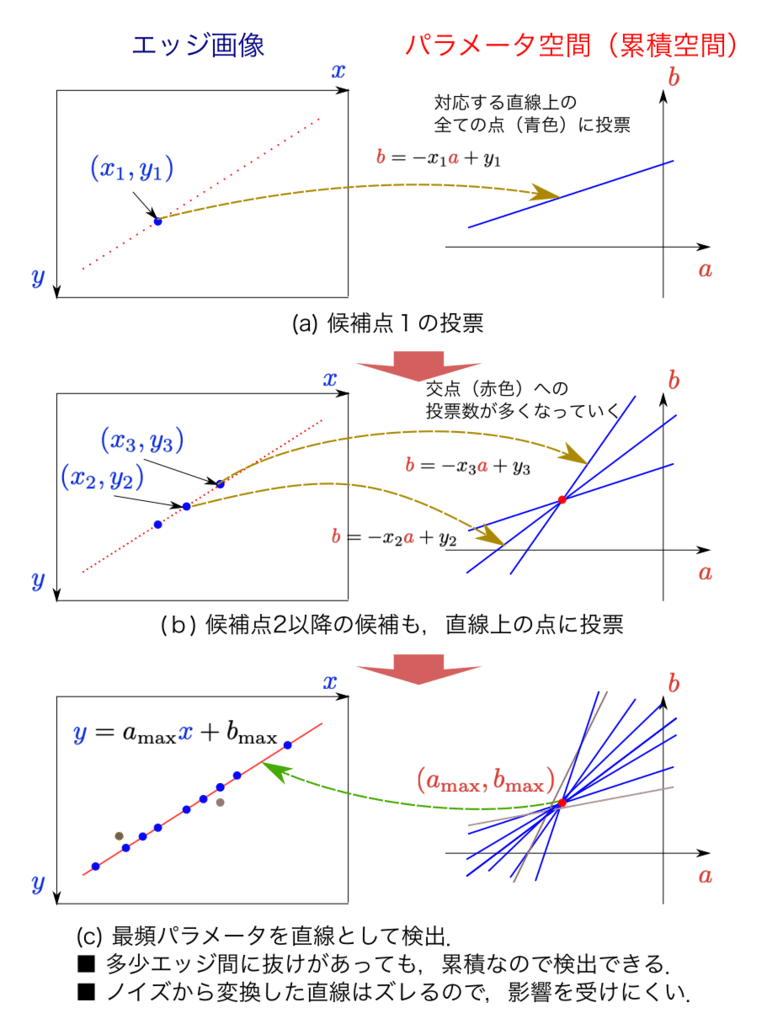
ハフ変換
- 直線や円などの幾何学的形状を画像から検出するための手法
- 極座標系で点Pを表現し、そのハフ空間の中から選出する手法
- Canny法でエッジを抽出した後処理することが多い
 V
V
エッジ検出
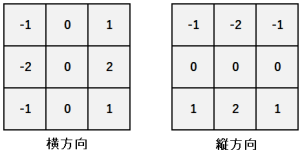
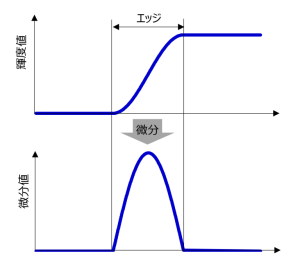
- canny法がよく使われる
- 仕組みはシンプルで次のようになる
- ガウシアンフィルターでデノイズ
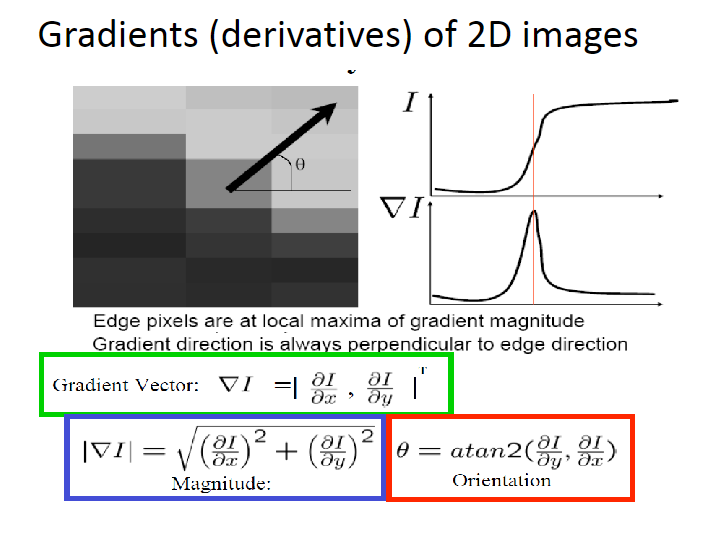
- Sobelフィルターを使って縦横のエッジを取得
- その強度(Edge Gradient / Manunitude)とOrientation(arctangentで)を求める
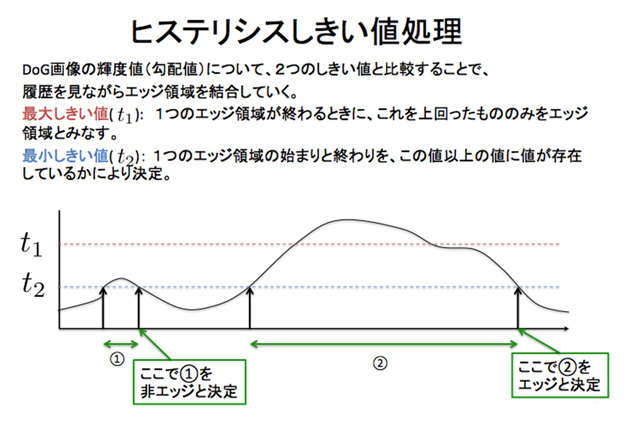
- その後、ヒステリシスによって連続性があり強度が出たものを線分と判断する
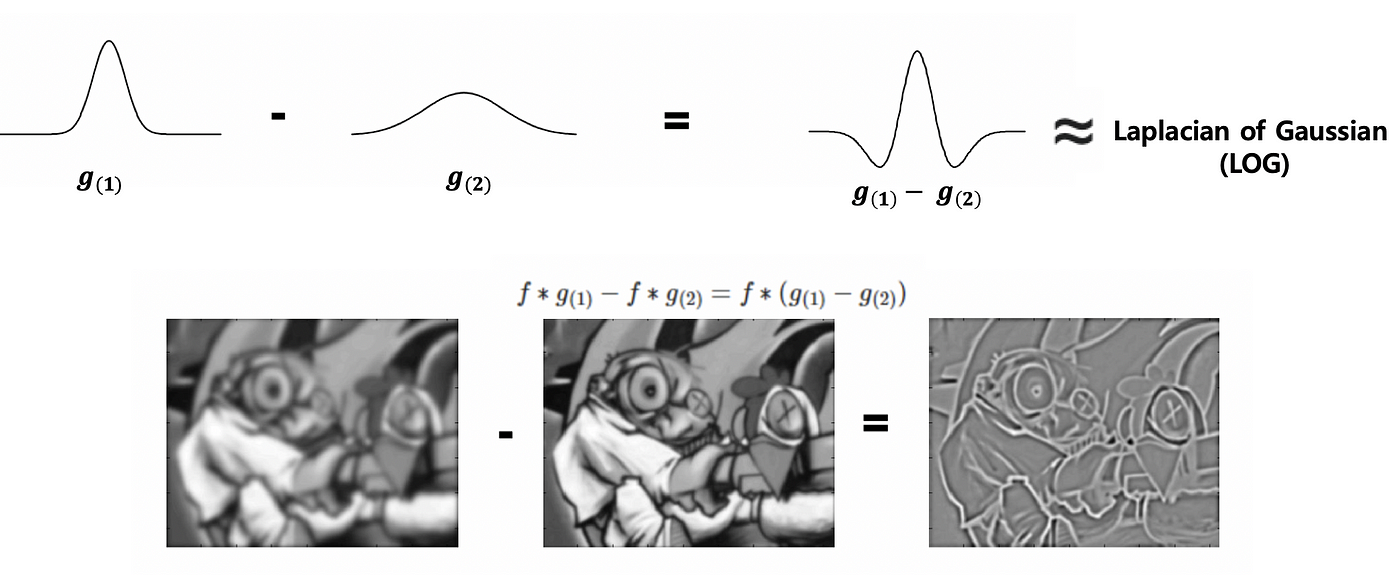
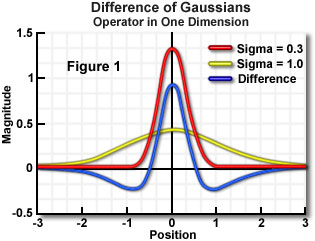
- DoG(Difference of Gaussian)
- ガウスフィルタを使って画像を2回平滑化し、その結果を減算する方法
- 1つは標準偏差が小さく、もう1つは標準偏差が大きいものを用いて、差で顕著化したフィルターを作って処理する
- ガウスフィルタによる平滑化を経ているため、ノイズに強い特性がある
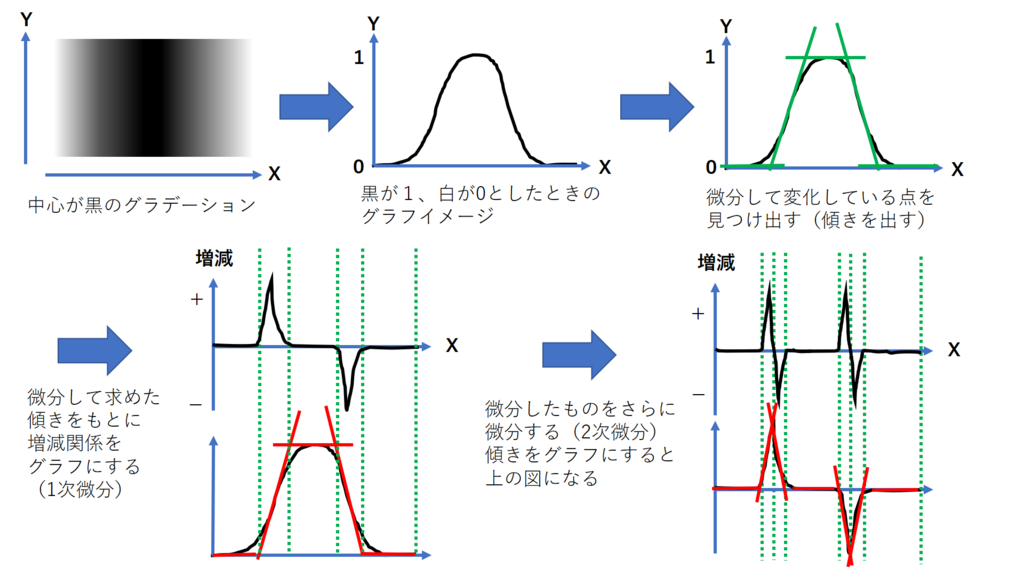
- LoG(Laplacian of Gaussian)
- ガウスフィルタとラプラシアンフィルタを用いていEdgeを強調する手法
- ラプラシアンフィルターは二階微分を計算する為のフィルタ
- ただし、ラプラシアンフィルタはノイズに弱いので、ガウスフィルタをかける
画像位置合わせ
画像位置合わせ(image registration)
- 画像位置合わせとは、2枚の画像の位置ずれを補正する処理のこと
- 画像位置合わせは、同じシーンの複数の画像を比較する時などに用いる
- 例えば、衛星画像解析やオプティカルフロー、医用画像の分野でよく登場する

画像位置合わせの例
テンプレートの特徴を取って、キーポイントとして、マッチングしてワープする処理。
| |



特徴量マッチング
特徴量の出し方
特徴量マッチングとは?
- 2つのオブジェクトで特徴量を抽出し、マッチングをする事
- 一番有名なのはテンプレートマッチング
一般的に、下のようなパイプラインになる。
- 2つの画像を用意する
- 特徴量detectorの処理
- まず、特徴点を出す
- その特徴点の特徴量を出す
- SIFTの場合は128次元
- 特徴量のmatcherの処理
- 2つの特徴量を変換する
- KDTree (木構造から検索)
- ブルーフォース (全部を検索)
- 検索する手法
- KNN法 (K個取得する)
- マッチのThresholding化
- 2つの特徴量が1以下など
- 2つの特徴量を変換する
特徴量
大域特徴量(global feature)とは
- 大域特徴量とは,画像全体から抽出される特徴量
- カラーヒストグラムなど
局所特徴量(local feature)とは?


マッチング手法
FLANN based Matcher
- FLANN: Fast Library for Approximate Nearest Neighborsの意味
- 特徴は名前の通り、approximateのNNを取り、BFMatcherより早く動く
- フロー
- Kd treeの構造を先にIndexとして作っておく。
- そこからKNNかFixed-Round KNNで木構造から検索する。(木の探索)
- KNNの場合は、近くのK個
- Fixed-Round KNNの場合は半径内にある全部
- とれたそれらのdiscriptorの距離を計算してあるパラーメター内の近さならそれをマッチした特徴としている
- BFMatcher
- 全部検索する
- なので、サブピクセルの特徴量が100で、基の特徴量が100とかの場合は、1万回もチェックする必要がある
FLANNの実装例
radius near neighborsとは?
- KNNの亜種。予め半径を決めておき、その範囲内をnear neibhbourにする
- K-nearestのestにならない理由は、何個かわからないから
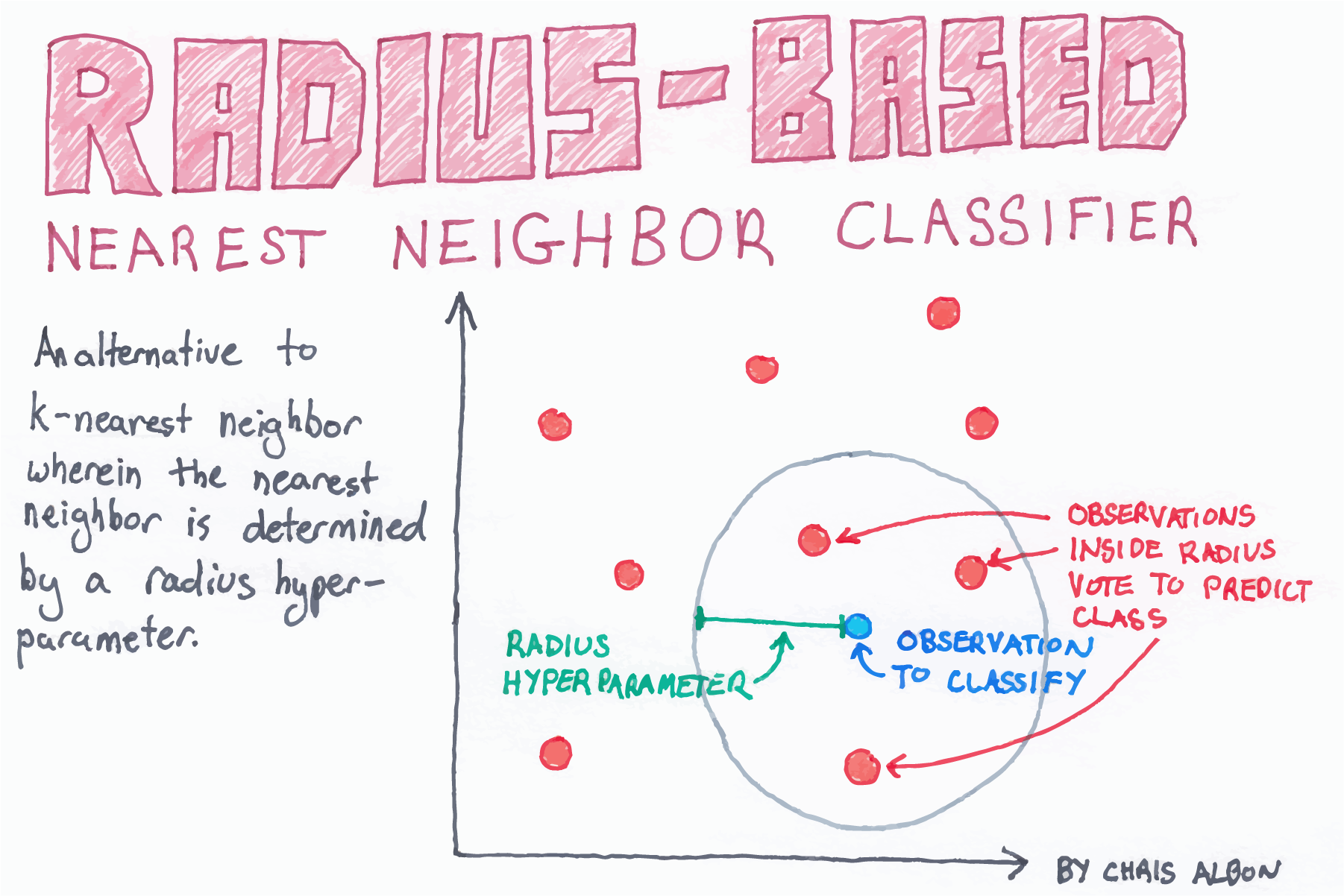
K-nearest neighbor searchとは?
- K個近くのデータを撮ってくる。それを基にデータを決める
- つまり、類は友を呼ぶ
KDTreeアルゴリズムとは?
- 決定木で作る
- 決定木の深さ=領域の個数=n^2
- バイナリツリーみたいな感じ
- KNNで近傍を探すのに、木構造を利用して探す
see Kd-treeと最近傍探索 適応システム特論・担当三上
KNNとFixed-Radius KNNの違いとは?
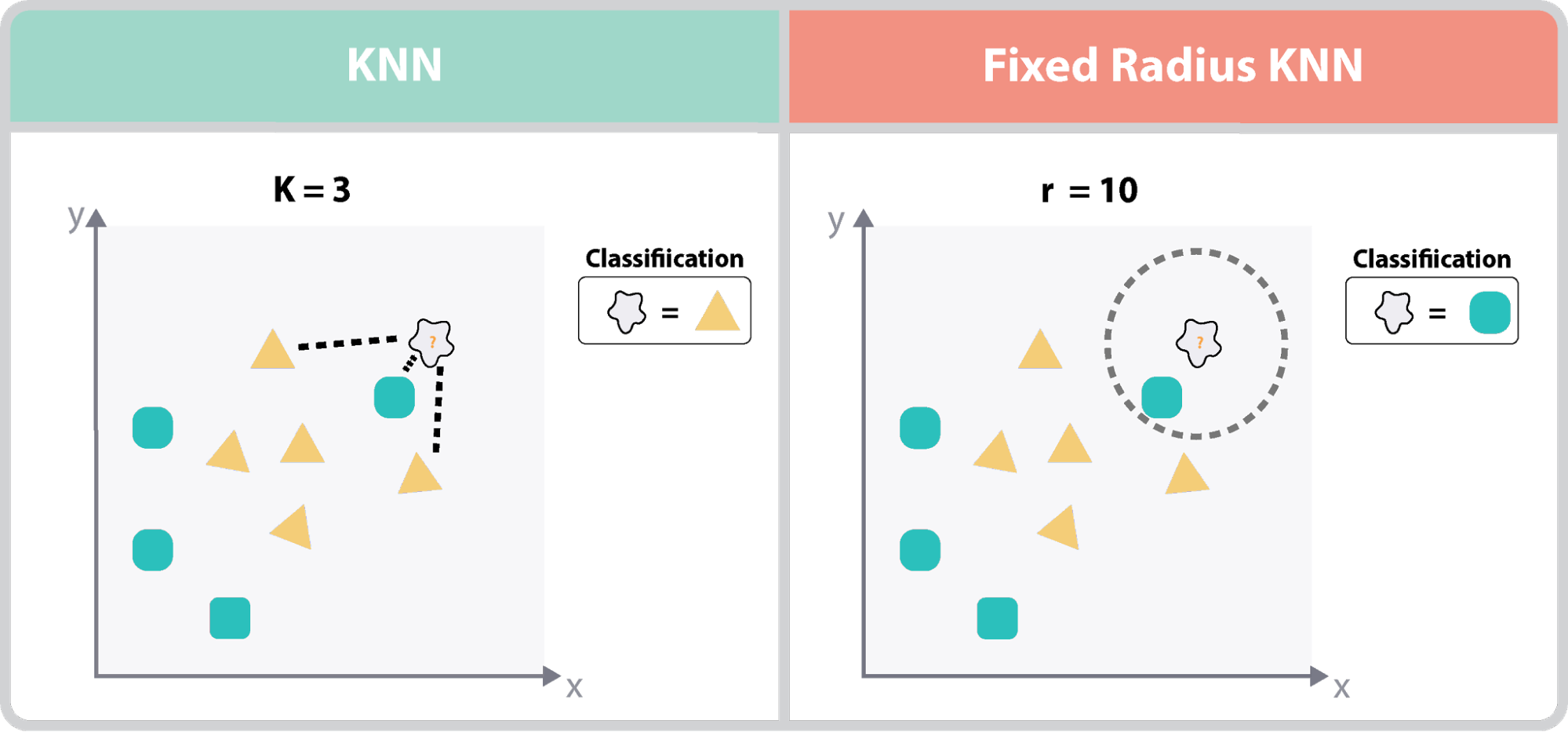
see https://ai-master.gitbooks.io/knn/content/simple-extensions.html
ブルーフォース法
Brute-Force matcher is simple. It takes the descriptor of one feature in first set and is matched with all other features in second set using some distance calculation. And the closest one is returned.
ブルートフォースマッチャーはシンプルで、最初のセットの1つの特徴の記述子を取り、距離計算を使用して2番目のセットの他のすべての特徴と照合する。そして、最も近いものが返される。これを繰り返す
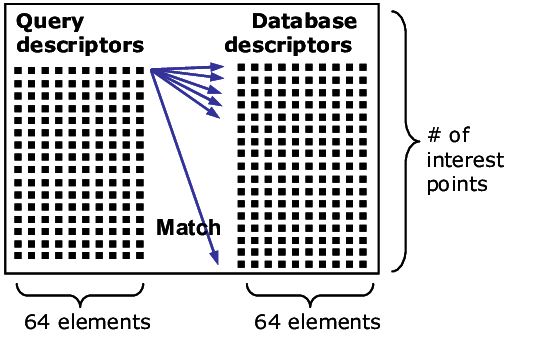
特徴量の比較

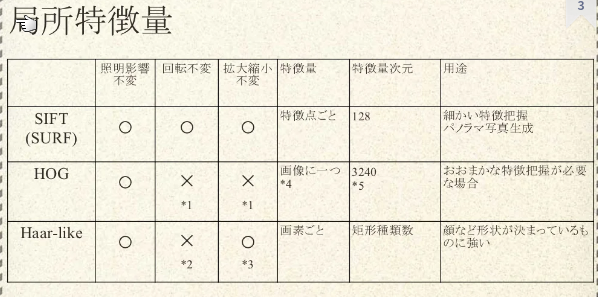
特徴量の出し方
Feature DetectorとFeature descriptorの違いは?
次のようにまとめられる。
| アルゴ | input | outputs | 特徴 | example |
|---|---|---|---|---|
| feature detector | image | locations (場所) | 特徴については教えてくれない | corner detector |
| feature descriptor | image | feature descriptors / feature vectors | 特徴について教えてくれる。scale invariantなことが多い。 | SHIFT, HOG, SURF, KAZE, AKAZE |
HOG特徴量とは?
- 勾配ベースの特徴量
- 白黒はっきりしていると取りやすい
- SVMを使ったりする
Haar like特徴量
- 隣接する2つの矩形の明るさの違い
- OpenCVだと顔認識に使われている
FAST algorithmとは?
binary string based
- BRIEF アルゴリズムとは?
- BRIEF (Binary Robust Independent Elementary Features, 二値頑健独立基本特徴)
- BRISKアルゴリズム
- Binary Robust Invariant Scalable Keypoints (BRISK) アルゴリズム
- BRIEFを発展させた以下のような方法で、スケール不変性と回転不変性を得ているのがBRISKである
- ORB Detector(Oriented FAST and rotated BRIEF)
- OrientedFASTおよびrotatedBRIEFは、Ethan Rubleeetalによって最初に発表された高速で堅牢なローカル機能検出器
変換
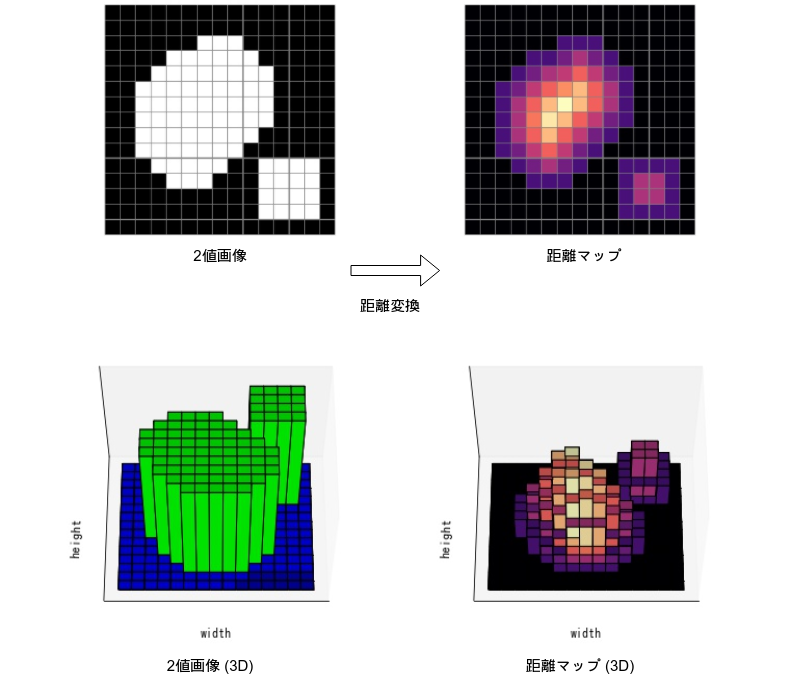
距離変換
距離変換 (distance transform) とは、2値画像を入力としたとき、各画素の最も近い画素値0までの距離を計算した 距離マップ (distance map) を作成する処理。dst = cv2.distanceTransform(src, distanceType, maskSize[, dst[, dstType]])で行う。
二値化
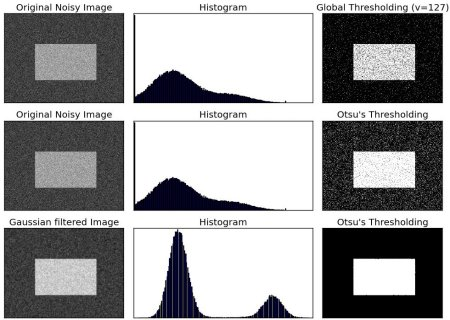
Otsu法
- ある画像を2値化(ピクセル値を255(最大値)or 0(最小値)にする = バイナリー化 = ざっくり言うなら白黒化)にする場合、その閾値を決定する必要がある
- Otsu法は画像の輝度ヒストグラムを元に、いい感じの閾値を自動で決定してくれるアルゴリズム
- ただし、ヒストグラムが大きく二つに別れるところをバッツリと二つに分ける(=閾値を決定する)アルゴリズムなので、そういった双峰性を持たないヒストグラムに対してはうまく閾値を決定できないらしい
pタイル法
Pタイル法(Percentile Method)は、2値化したい領域が全データの領域に占める割合をパーセント(%)で指定し2値化する手法。
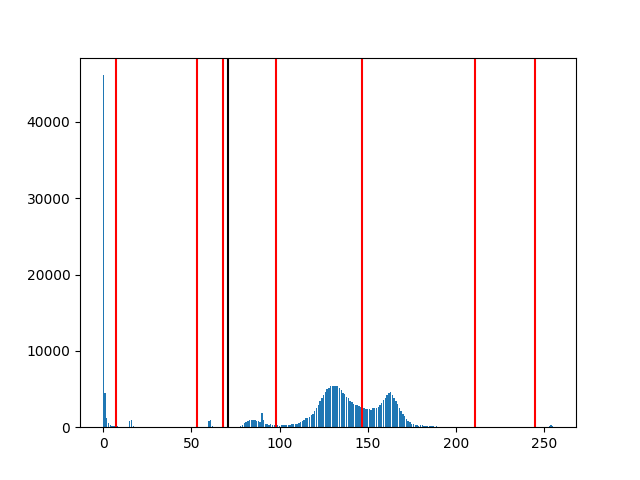
Multilevel Thresholding
Otsuの二値化と違い、複数のThreasholdでクラスタリングできる。
adaptive thresholding
- 画像中の小領域ごとにしきい値の値を計算する
- そのため領域ごとに光源環境が変わってしまうような画像に対して、単純なしきい値処理より良い結果が得られる

モルフォロジー変換
モルフォロジー変換とは?
- 与えられた2値画像または濃淡画像からの特徴抽出を目的とした図形変形手法の理論体系
- 画像のノイズ除去,平滑化,形状記述,テクスチャ解析,細線化処理などに用いられる.
- Dilation, Erosion, Opening, Closingの基本演算と、
- モルフォロジーグラジエント(Dailationした画像からErosionした画像を減算することで,エッジを検出する)
- トップハット変換(元画像からOpeningした画像を減算する)
- ブラックハット変換(Closingした画像から元画像を減算する) の7種類
- 要は、以下の画像のように、対象画像を太くしたり補足したり、それらを組み合わせたりして目的のオブジェクトを取り出す方法(画像は上記リンクより拝借)

ある特徴的なオブジェクトを検出するのに使える。
see Hands-on Morphological Image Processing
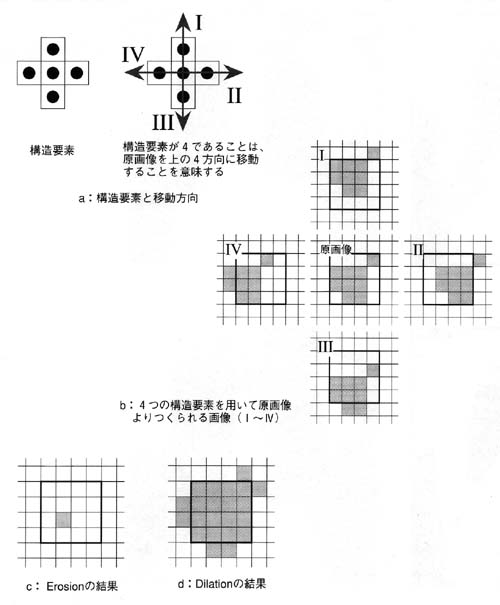
モルフォロジ処理の具体的な処理とは?
- モルフォロジ処理は、“構造要素"と呼ばれる画像を移動させる要素と,“ミンコフスキー(Minkowski)和・ミンコフスキー差” と呼ばれる演算から成り立っている
- モルフォロジー処理における代表的な処理は、「Erosion(エロージョン)」と「Dilation(ダイレーション)」と呼ばれる処理
- それぞれ孤立点の除去,不連続な点の接続と穴埋めのために利用される
- Erosionで細くしてノイズを減らして、Dilationで大きくして元の大きさに戻すイメージ
- opening
- erosionの後にdilationなので、ノイズが消える
- closing
- dilationのあとにerosionなので、ノイズが増える
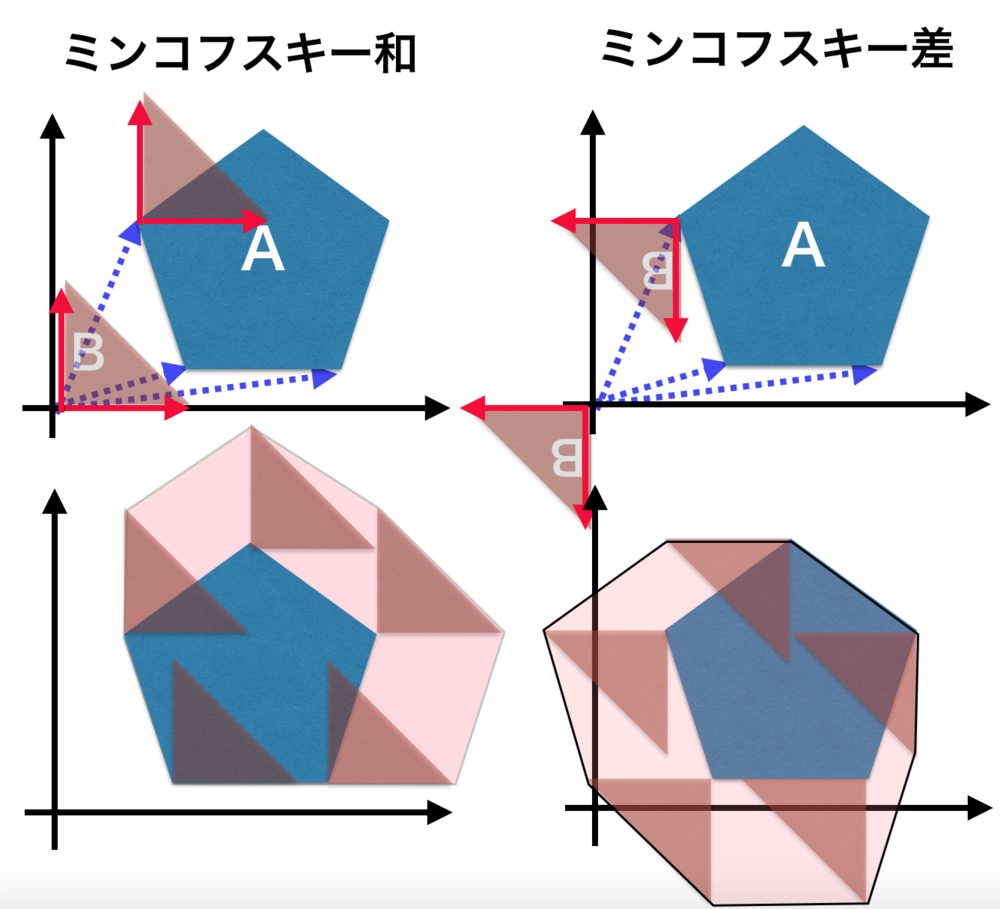
ミンコフスキー和と差
- ミンコフスキー和・差は、二つのベクトルの集合同士を使って新しいベクトルの集合を求める.
- このミンコフスキー和と差を用いることで、ゲームにおける衝突判定やロボットのモーションプログラミングで計算を簡単にできる.
ワープ処理 (Image warping)

幾何学的変換(Geometric Transformation)
- 幾何学的変換は集合の何らかの幾何学的な構造を持つ自身への(もしくは幾何学的な構造を持つ相異なる集合への)全単射
- アフィン変換も幾何学的変換の一つ

統計的にノイズを消す方法
| |

画素補間法(image interpolation)
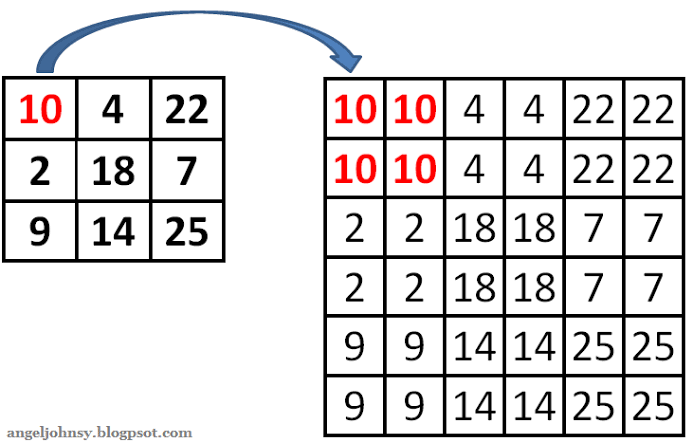
- nearest neighbor interpolation
- 最近傍補間法とも
- コンピューターによる画像処理で、画像の回転・拡大・変形を行うときの画素補間法の一つ
- 求めたい画素に最も近い位置の画素の情報を参照して補間する
バイキュービック法
- コンピューターによる画像処理で、画像の回転・拡大・変形を行うときの画素補間法の一つ
- 求めたい画素の周辺の4×4画素(16画素)の輝度値を参照し、三次式で近似して補間する
- 濃淡や色の急激な変化を再現するのに適するが、計算に時間を要する
バイリニア法(bilinear interpolation)
- コンピューターによる画像処理で、画像の回転・拡大・変形を行うときの画素補間法の一つ
- 求めたい画素の周辺の2×2画素(4画素)の輝度値を参照し、その加重平均値を用いて補間する

距離
分布の距離
2つの分布間の距離を出すKL距離などは厳密には距離ではないが、距離と言う。
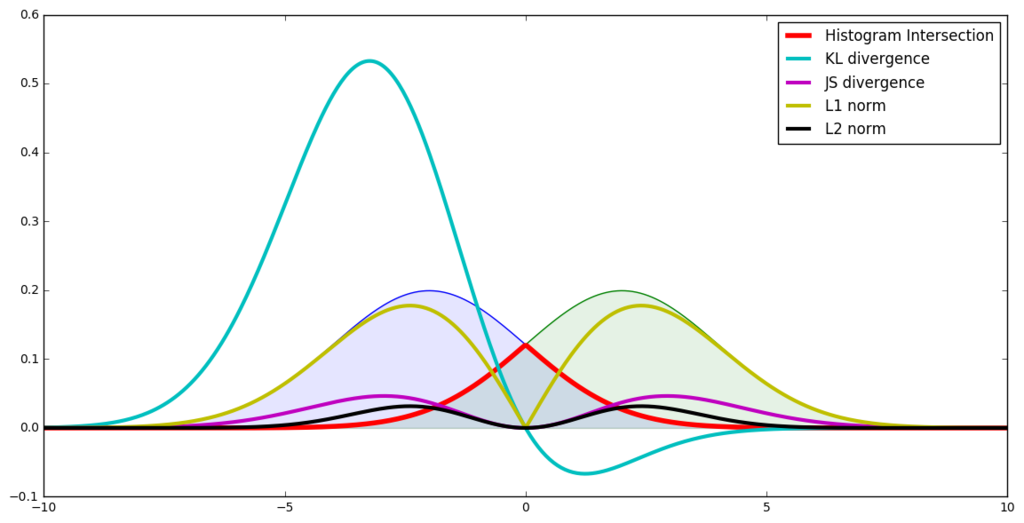
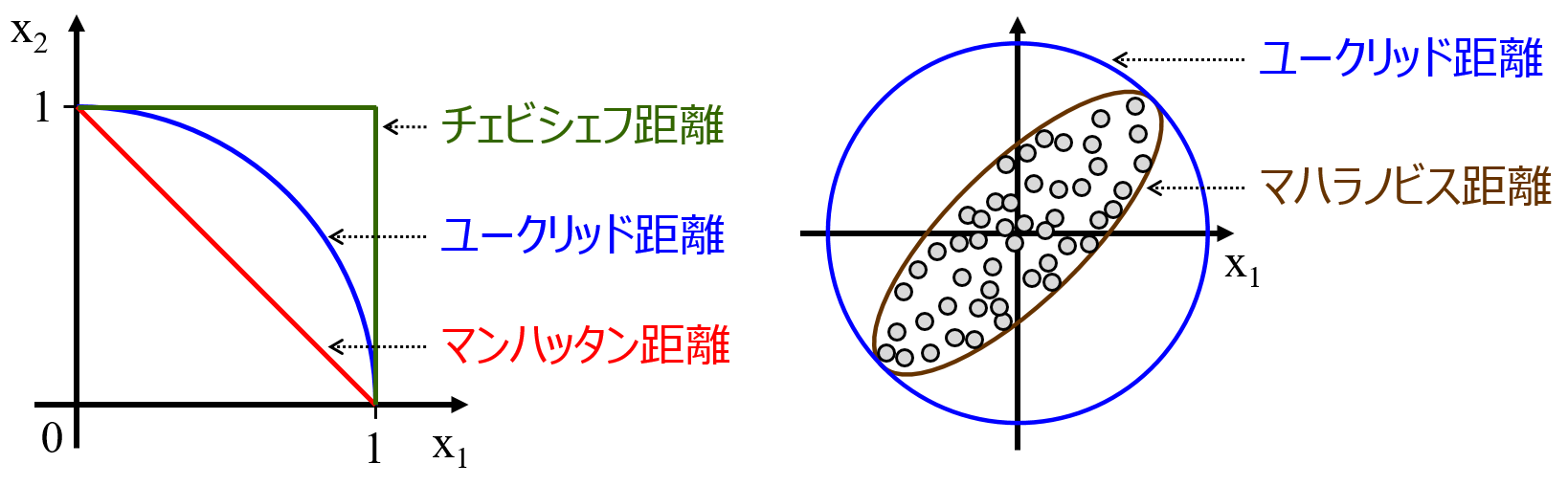
一般的な距離
- マンハッタン距離
- ユークリッド距離
- マハラノビス距離
- チェビシェフ距離
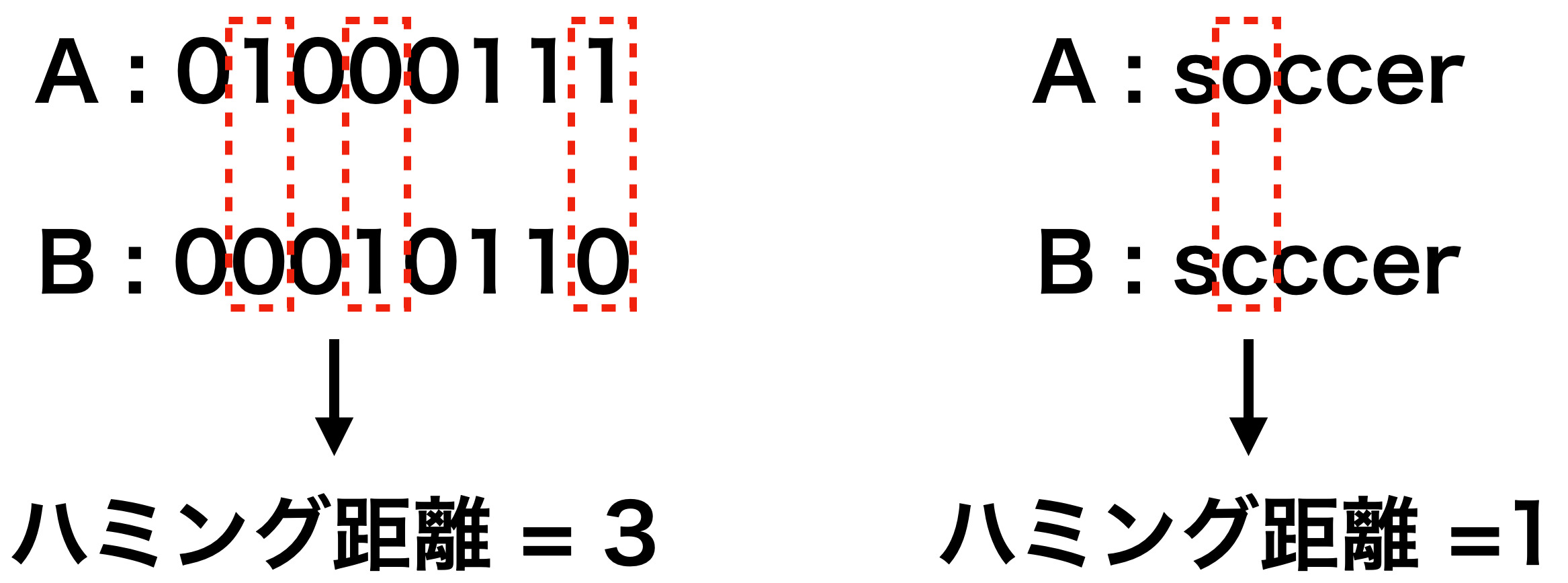
文字列間の距離
OCR後の文字列間の距離比較を行うには、次の距離が有名。
- ハミング距離
- 同じ文字数の文字列の距離
- レーベンシュタイン距離
- 別々の文字数の文字列の距離
円
Circle, Curve, Arc, Fircleの違い
- Circle: 円
- Curve: 曲線
- Arc: 円弧
- Fircle: 手書きの円
メモ
- トポロジー的には、Arcは図形では、凸
- Circle -> D Cut -> Squaireのように相が変換する
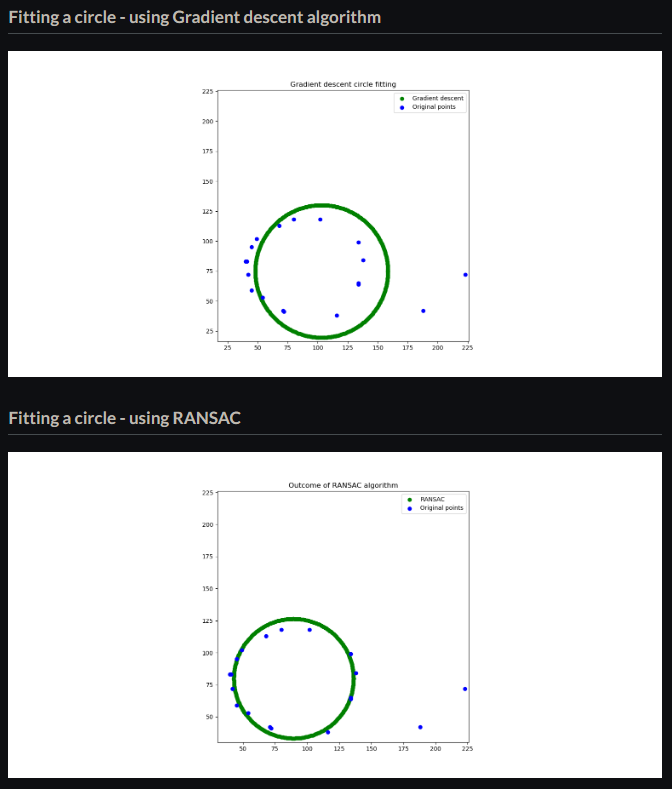
RANSAC algorithmでArcフィッティング
The RANSAC (Random sample and consensus) algorithm is the gold standard in eliminating noise.
アルゴのフロー
- データをランダムにサンプリングする.(非復元抽出)
- モデルを学習する
- 全てのデータに対して誤差を計算する
- 3で求めた誤差から正常値と外れ値を決める
- 正常値のみでモデルの性能を評価する
- 既定回数に達したら終了.そうでなければ1に戻る
ようは、アンサンブル学習のbaggingをしている。
RANSACとGradient descent algoの違い。
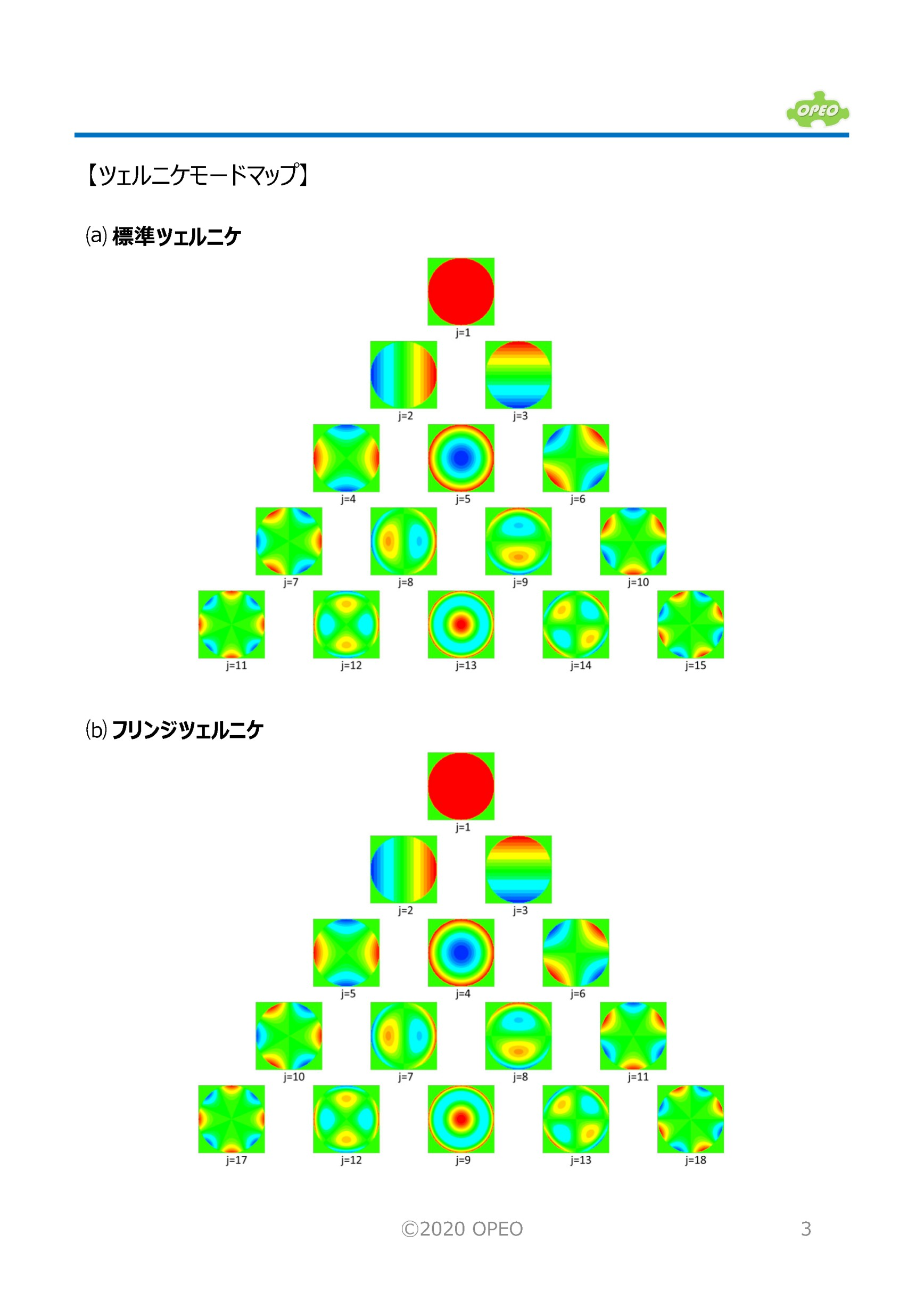
ゼルニケ多項式 (Zernike Polynomials)とは?
曲面を多項式で表現する手法の1つとして、光学設計ではZernike(ツェルニケ)多項式がよく使われる。詳細は以下のスライド。


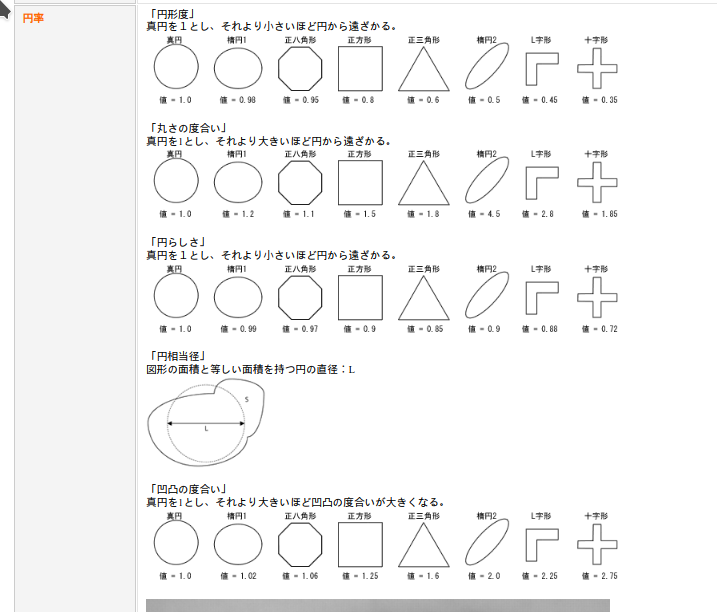
円形度
確か、円形度はISOで定義があったはず。
$$ 円形度 = \frac{4π \times S}{L^2} $$
(S = 面積, L = 図形の周囲長)

その例。
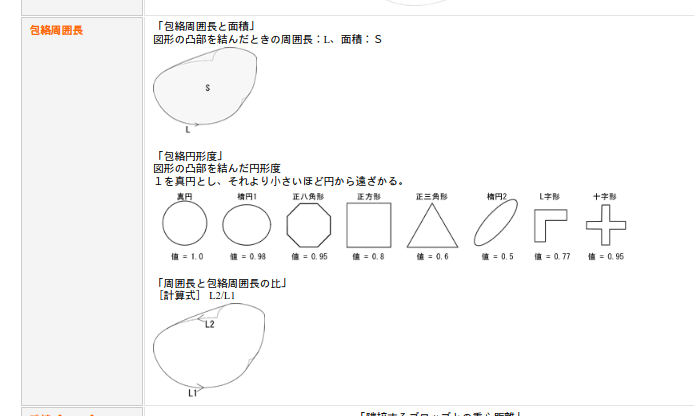
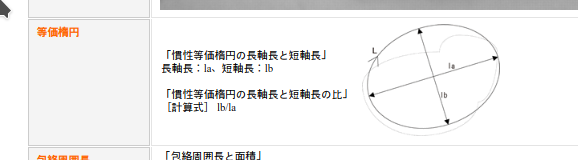
cv2で円形度。
| |
円摩度 (アスペクト比で補正した円形度)
see http://progearthplanetsci.org/highlights_j/072.html
New parameter of roundness R: Circularity corrected by aspect ratio.
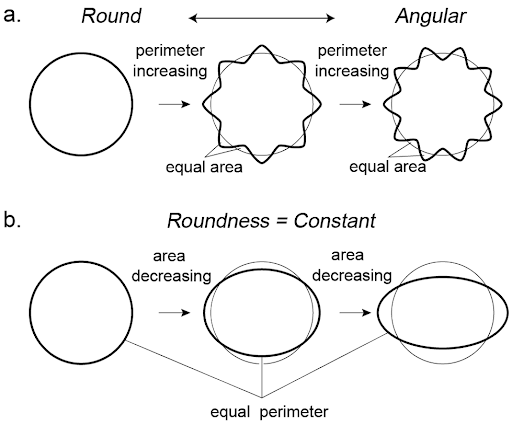
$$ R = Circularity + (Circularity_{perfect\_circle} - Circularity_{aspect\_ratio}) $$
ここで、
- $Circularity_{perfect\_circle}$
- 真円の円形度
- $Circularity_{aspect\_ratio}$
- 真円のアスペクト比のみを変化させたときに得られる円形度
円磨度 (psephicity) vs. roundness
- 円磨度 (psephicity)
- 礫(れき、小さい石のこと)または砂粒の円味を帯びる程度。
- 通常は構成岩石の比重と硬度との比をもって円磨率(coefficient of psephicity)という。
- rounhdness
- 砕屑物が川や海によって運搬される過程で破壊され摩滅によって次第に角や稜がとれて円い礫となる
円磨度の区分(Pettijohn : 1957)
- 角(angular,円磨度 : 0~0.15)
- 亜角(subangular,円磨度 : 0.15~0.25)
- 亜円(aubrounded,円磨度 : 0.25~0.40)
- 円(rounded,円磨度 : 0.40~0.60)
- 十分に円磨(well-rounded,円磨度 : 0.60~1)
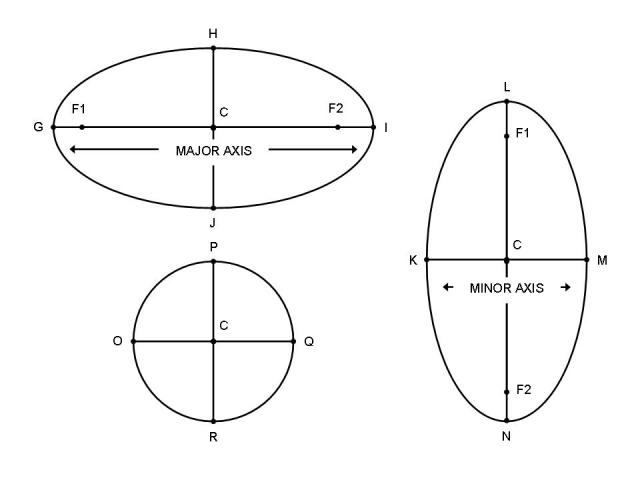
楕円の歪み度
Major AxisとMinor Axisの比を取ればOK。
モーメント
Huモーメントは次の3つに対して不変な特徴を持つ。
- 平行移動 (translation)
- スケール (scale, size)
- 回転 (rotation)
モーメント (素モーメント)
2変数関数$f(x,y)$に対して、$(p+q)$次のモーメント(素モーメント)を次のように定義する。 pとqはそれぞれモーメントの次数。
$$ {M_{pq} = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x^p y^q f(x,y) dx dy } $$
これをグレースケールの画像に適用すると
$$ {M_{ij} = \sum_{x} \sum_{y} x^i y^j I(x,y)} $$
つまり、$x座標 \times y座標 \times ピクセルの値$の合計値となる。 素モーメントそのものは不変量ではない。
$$ {\begin{align} M_{00} &= 面積, \\ M_{01} &= Y軸座標値とピクセル値の面積=Y軸座標値の期待値, \\ M_{10} &= X軸座標値とピクセル値の面積=X軸座標値の期待値, \\ M_{11} &= XY軸座標値とピクセル値の体積=XとY軸座標の面積, \\ M_{20} &= Y軸座標値^2とピクセル値の面積=Y軸座標^2の期待値, \\ M_{02} &= X軸座標値^2とピクセル値の面積=X軸座標^2の期待値, \\ \end{align}} $$
- $M_{00}$の解釈
- すると、$M_{00}$などは、面積と捉えられる。
- また、ピクセル値を確率と捉えると、面積ではなく、確率和と理解できる。
- $M_{01}$ の解釈
- $M_{01}$はY軸座標値とピクセル値の掛け算=その面積。
- ただし、ピクセル値の値域[0,1]なので、確率と捉えると、
- Y座標値の期待値の合計=期待値和 $$ 期待値=確率 \times 確率変数 $$
- 合計なので、単位は$Count \times Expected Value$
- $M_{11}$の解釈
- $M_{11}$はXY軸座標値とピクセル値の掛け算=その体積。
- ただし、ピクセル値の値域[0,1]なので、確率と捉えると、
- Y座標値の期待値とX軸座標値の期待値の積の合計=期待値積の和=混合分布の和
- $M_{02}$の解釈
- $M_{02}$はY軸座標値^2とピクセル値の掛け算=その体積。
- ただし、ピクセル値の値域[0,1]なので、確率と捉えると、
- Y座標値^2の期待値の合計=期待値平方和
中心モーメント(並行不変性)
中心モーメントは平行普遍性をもつ。 なぜこの中心モーメントが並行不変性をもつかというと、ピクセル座標の原点を物体の中心(重心)にしているから。 なので、物体がどこにあろうが、同じ値を出す=並行不変値
$$ {\mu_{ij} = \sum_{x} \sum_{y} (x-\bar{x})^i (y-\bar{y})^j I(x,y) } $$
ただし、$\bar{x},\bar{y}$は先に示した重心を示す。
この$\mu$のパターンを定義すると以下。
$$ {\begin{align} \mu_{00} &= M_{{00}}, \\ \mu_{01} &= 0, \\ \mu_{10} &= 0, \\ \mu_{11} &= M_{{11}}-{\bar {x}}M_{{01}}=M_{{11}}-{\bar {y}}M_{{10}} , \\ \mu_{20} &= M_{20}-{\bar {x}}M_{10}, \\ \mu_{02} &= M_{02}-{\bar {y}}M_{01}, \\ \end{align}} $$
- $\mu_{01}$の解釈
- $\mu_{01}=0$の理由は$\bar{y}$がY軸の重心ピクセル座標であり、
- $y-\bar{y}$の値は+と-で分布して合計すると必ず0になるから。
- ※ 重心はピクセルのブロブの原点。
- $\mu_{11}$の解釈
- つまり、あるピクセルの値(確率)とそのピクセルの座標の原点からの距離を加味した指標
- $\mu_{20}$の解釈
- 重心から座標がどれだけ離れているか、ただし、二乗しているので、絶対値。
- つまりは、重心からどれだけはなれているかを加味した値。
スケール不変性
次のような値を考えることで、スケールに対する不変量を作ることができる。 このモーメントは$i+j≥2$のとき並進不変性を持つ。 なぜ、スケール普遍化というと、分母に面積を撮っているから。つまり、単位面積あたりの値にしている。
$$ {\eta _{{ij}}={\frac {\mu _{{ij}}}{\mu _{{00}}^{{\left(1+{\frac {i+j}{2}}\right)}}}} } $$
- $i+j<2$の理由
- 上の定義を代入してみるとわかるが、$i+j<2$のときは定数になってしまい意味を持たない。
- なぜなら、下のように、$\mu$のijの合計が2未満のときは、分母を加味して定数だから。 $$ {\begin{align} \mu_{00}=面積 \\ \mu_{10}=0 \\ \mu_{01}=0 \\ \end{align}} $$
- $\eta_{11}$の解釈 $$ {\begin{align} i=1 \\ j=1 \\ \eta_{ij}=\frac{\mu_{11}}{\mu_{00}^2} \end{align}} $$
- $\eta_{20}$の解釈 $$ {\begin{align} i=2 \\ j=0 \\ \eta_{ij}=\frac{\mu_{20}}{\mu_{00}^2} \end{align}} $$
回転不変性
- 更に$\eta{ij}$を用いて、回転に対して不変な量を構築することができる。これはHuによって発見されたため、Huモーメント不変量と呼ばれている
- 1から6までは回転不変。7はskew invariant
$$ I_{1} = \eta _{{20}}+\eta _{{02}} \\ $$
$$ I_{2} = (\eta _{{20}}-\eta _{{02}}) ^{2}+4 \eta _{{11}}^{2} \\ $$
$$ I_{2} = (\eta _{{20}}-\eta _{{02}})^{2}+4\eta _{{11}}^{2} \\ $$
$$ I_{3} = (\eta _{{30}}-3\eta _{{12}})^{2}+(3\eta _{{21}}-\eta _{{03}})^{2} \\ $$
$$ I_{4} = (\eta _{{30}}+\eta _{{12}})^{2}+(\eta _{{21}}+\eta _{{03}})^{2} \\ $$
$$ I_{5} = (\eta _{{30}}-3\eta _{{12}})(\eta _{{30}}+\eta _{{12}})[(\eta _{{30}}+\eta _{{12}})^{2}-3(\eta _{{21}}+\eta _{{03}})^{2}]+(3\eta _{{21}}-\eta _{{03}})(\eta _{{21}}+\eta _{{03}})[3(\eta _{{30}}+\eta _{{12}})^{2}-(\eta _{{21}}+\eta _{{03}})^{2}] \\ $$
$$ I_{6} = (\eta _{{20}}-\eta _{{02}})[(\eta _{{30}}+\eta _{{12}})^{2}-(\eta _{{21}}+\eta _{{03}})^{2}]+4\eta _{{11}}(\eta _{{30}}+\eta _{{12}})(\eta _{{21}}+\eta _{{03}}) \\ $$
$$ I_{7} =(3\eta _{{21}}-\eta _{{03}})(\eta _{{30}}+\eta _{{12}})[(\eta _{{30}}+\eta _{{12}})^{2}-3(\eta _{{21}}+\eta _{{03}})^{2}]-(\eta _{{30}}-3\eta _{{12}})(\eta _{{21}}+\eta _{{03}})[3(\eta _{{30}}+\eta _{{12}})^{2}-(\eta _{{21}}+\eta _{{03}})^{2}]. \\ $$
Humomentの例
シンプルなHumomentによる類似画像検索。
| |

| Lenna.png | Lena3.jpg | sendo1.jpg | Sendou2.jpg | monnalisa.jpg | apple.jpg | Red_Apple.jpg |
|---|---|---|---|---|---|---|
| Lenna.png | 0.00 | 0.04 | 5.93 | 5.87 | 4.19 | 2.43 |
| Lena3.jpg | 0.04 | 0.00 | 5.93 | 5.86 | 4.22 | 2.41 |
| sendo1.jpg | 5.93 | 5.93 | 0.00 | 0.09 | 7.82 | 4.55 |
| Sendou2.jpg | 5.87 | 5.86 | 0.09 | 0.00 | 7.86 | 4.47 |
| monnalisa.jpg | 4.19 | 4.22 | 7.82 | 7.86 | 0.00 | 3.97 |
| apple.jpg | 2.43 | 2.41 | 4.55 | 4.47 | 3.97 | 0.00 |
| Red_Apple.jpg | 4.83 | 4.83 | 1.19 | 1.11 | 7.88 | 4.94 |
画像のモーメントと面積と重心
モーメントとは?
$$ M_{nm} = \sum^{画像全体} (x座標^{n} \times y座標^{m} \times 画素値) $$
画像中の全ピクセルについての総和。
モーメントのフロー
モーメントの計算方法は2つのフローに従う。
- ピクセルずつデータを取る
- 座標ごとのべき乗をもとめて足す
まず、データ(x座標、y座標、画素値)を調べる
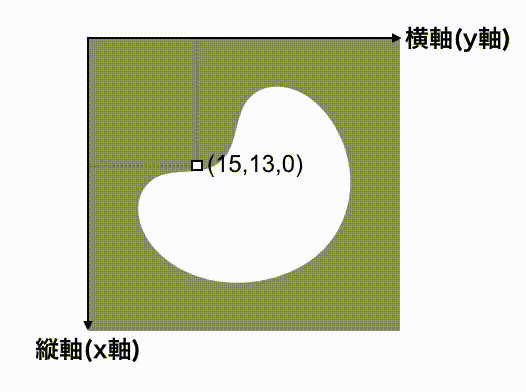
次に、全てのピクセルについて次を求める。
- x座標のn乗
- y座標のm乗
さらに、上記の2つと画素値(0または1)を掛け合わせる。
例えば、(15,17,1)のピクセルについて、n=2、m=0の場合は次となる。
$$ M_{2,0} = 15^{2} \times 17^{0} \times 1 = 225 \times 1 \times 1 = 225 $$
このピクセルでの計算結果は225となる。
全てのピクセルでの計算結果を足し合わせたものが画像のモーメント$M_{nm}$。
$M_{0,0}$が面積になる理由
- 白ピクセル(1)の場合 $$ M_{0,0} = 15^{0} \times 17^{0} \times 1 = 1 \times 1 \times 1 = 1 $$
- 黒ピクセル(0)の場合 $$ M_{0,0} = 15^{0} \times 17^{0} \times 0 = 1 \times 1 \times 0 = 0 $$
- つまり、白のピクセルの個数=面積がもとまるから。
$(\frac{M_{10}}{M_{00}}, \frac{M_{01}}{M_{00}})$で重心になる理由
- Xを考えると、
- 白ピクセル(1)の場合 $$ M_{1,0} = 15^{1} \times 17^{0} \times 1 = 15 \times 1 \times 1 = 15 $$
- 黒ピクセルの場合 $$ M_{0,0} = 0 $$
- 分母は次になる $$ M_{0,0} = 面積 $$
単純化すると次になる。
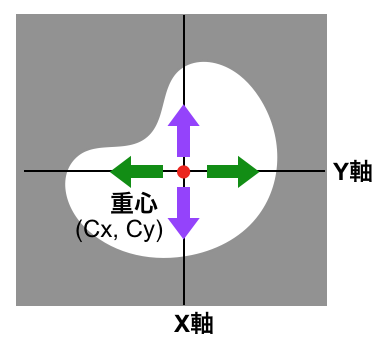
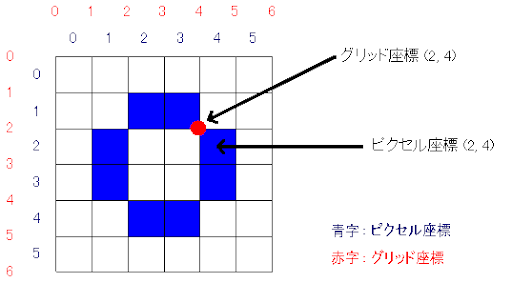
- 画像なので座標はピクセル座標
- (0,0), (2,2)の範囲のピクセルを考える
- つまり、範囲はグリッド座標でいう、(0,0) から (3,3)までのブロブ
- 面積は9
- $M_{0,0}$ = 9
- $M_{1,0}$= 0+1+2+0+1+2+0+1+2 = 9 (左上から横方向にチェック)
- $\frac{M_{10}}{M_{00}}$=9/9=1
つまり、X座標では1の座標をもつピクセルが重心。 また、重心=ブロブの原点。 つまり、重心を原点ととると、全てのx座標の合計、全てのy座標の合計のそれぞれが0となる。
Contour(輪郭)
contourとperimeterの違い
- perimeter: 周囲
- contour: 輪郭
Contourのフロー
- グレースケールに変換
- 画像を2値化する
- 輪郭の取得
- 輪郭の分析
例
| |
Contourから取れるモノ
- 面積(
cv2.contourArea) - サイズ(
cv2.boundingRect) - 点の数
- 領域を囲む周囲長(
cv2.arcLength) - 領域を塗りつぶし(
cv2.drawContours) - 少ない座標で輪郭(
cv2.approxPolyDP) - 輪郭の近似による輪郭の取得(
cv2.approxPolyDP(cnt,0.1*cv2.arcLength(cnt,True),True)) - 凸包による図形判別(
cv2.convexHull) - 外接矩形による角度取得(
cv2.minAreaRect) - 輪郭の類似度の計算(
cv2.matchShapes) - 重複したcontoursのマージ(
NMS:Non-Maximum Suppression的な) - 隣接するcontoursのマージ(
階層クラスタリング)
findContoursの引数
- binaryデータを渡して、その中のオブジェクトを取得するメソッド
- 簡易的物体検知であり、以外に複雑な構造をしているのでメモ
- 手法(mode)+輪郭取り方(method)でパターンが分かる

NOTE: 外の白枠は分かりやすさでついているもので、実際はない。
findCountoursのmode
RETR_TREE: 輪郭の階層情報をツリー形式で取得する。
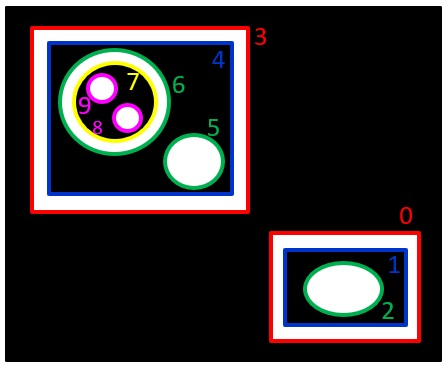
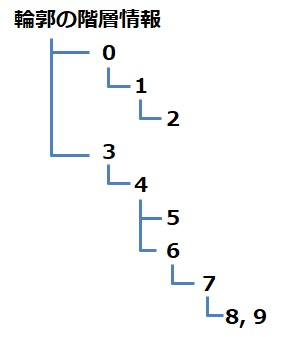
RETR_CCOMP:白の輪郭の外側と内側の輪郭を構造化する
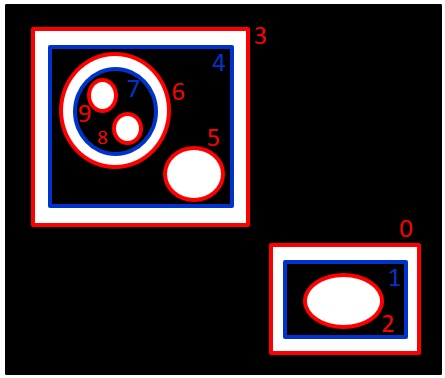
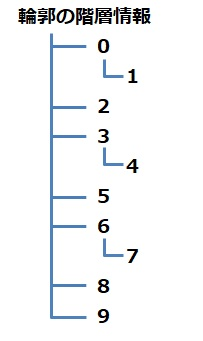
RETR_LIST:階層なし
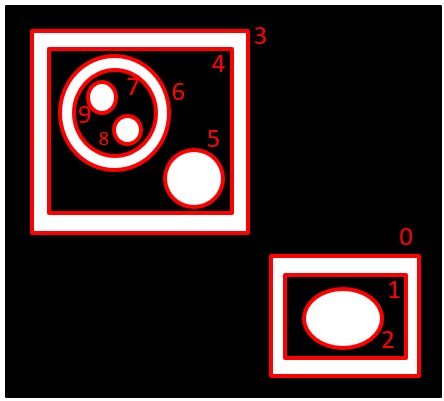

RETR_EXTERNAL:外側のみ

findCountoursのmethod
CHAIN_APPROX_NONE:輪郭上のすべての座標を取得
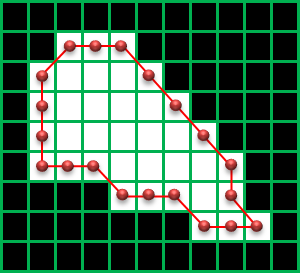
CHAIN_APPROX_SIMPLE:縦、横、斜め45°方向に完全に直線の部分の輪郭の点を省略
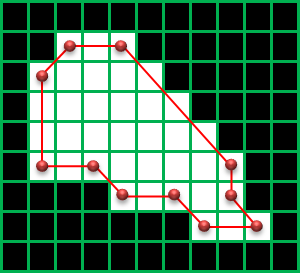
CHAIN_APPROX_TC89_L1, CHAIN_APPROX_TC89_KCOS:輪郭の座標を直線で近似できる部分の輪郭の点を省略
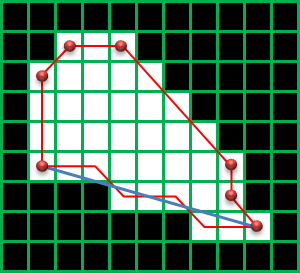
findContoursの戻り値
methodの設定により輪郭番号があったりなかったりするが、大体contoursは次の構造を取る。
| |
minとmaxで4点のcontourを作る例。
| |
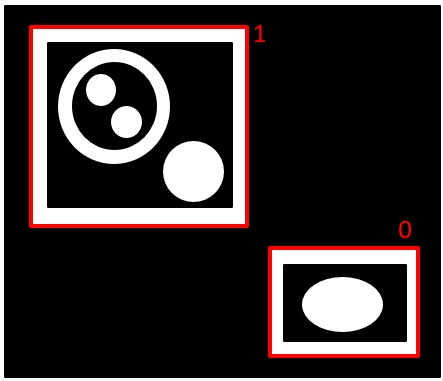
hierarchyは次の構造を取る。
| |
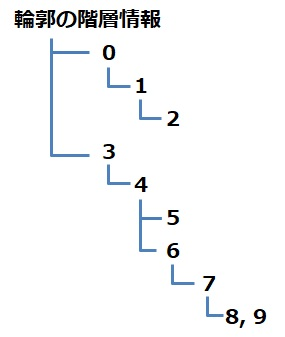
上の場合は下になる。
分かりやすく言うと、階層的には、下、上、右、左の順番。
| |
Floodfill
- 他の物体検知手法としては、Floodfillもある
- seedPoint に指定した画素と画素値の差が指定範囲内の画素を同じグループ (連結成分) と見なして塗りつぶしを行う
- loDiff(下限)とupDiff(上限)をつけて塗りつぶすアルゴ
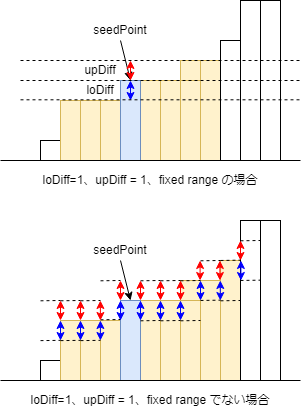
オプティカルフロー
- 物体の移動軌跡を行うのに使う手法
- 動画像中のフレームで、移動体上の各点の移動方向と移動距離を表す量である動きベクトルを計算する
- 物体トラッキングでは、カルマンフィルタを使って予測することも行う

ガイド
Scikit learn ガイド
有名なScikit-leranのガイド。
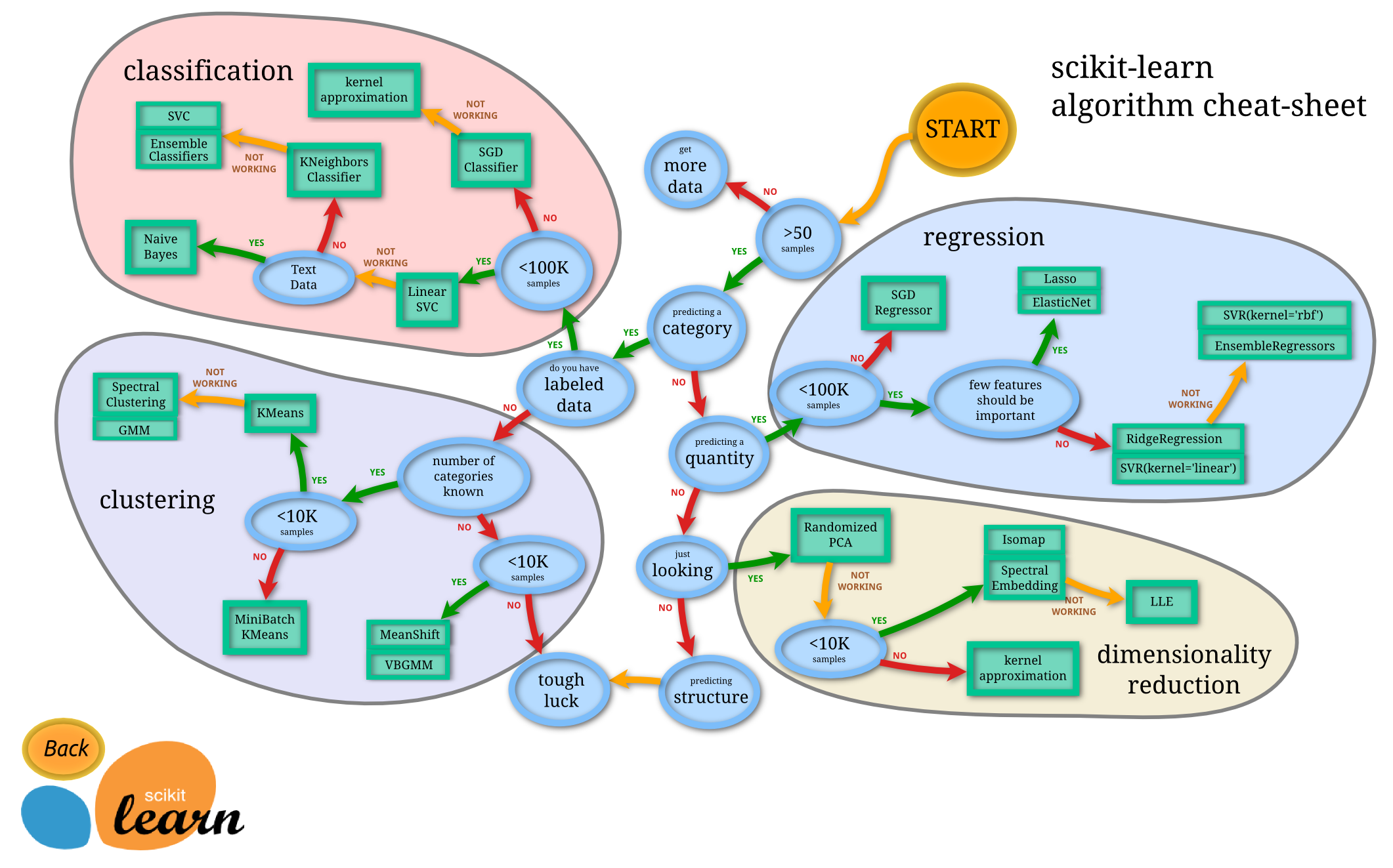
Dlib選択ガイド
こちらは一部で有名なDlibガイド。
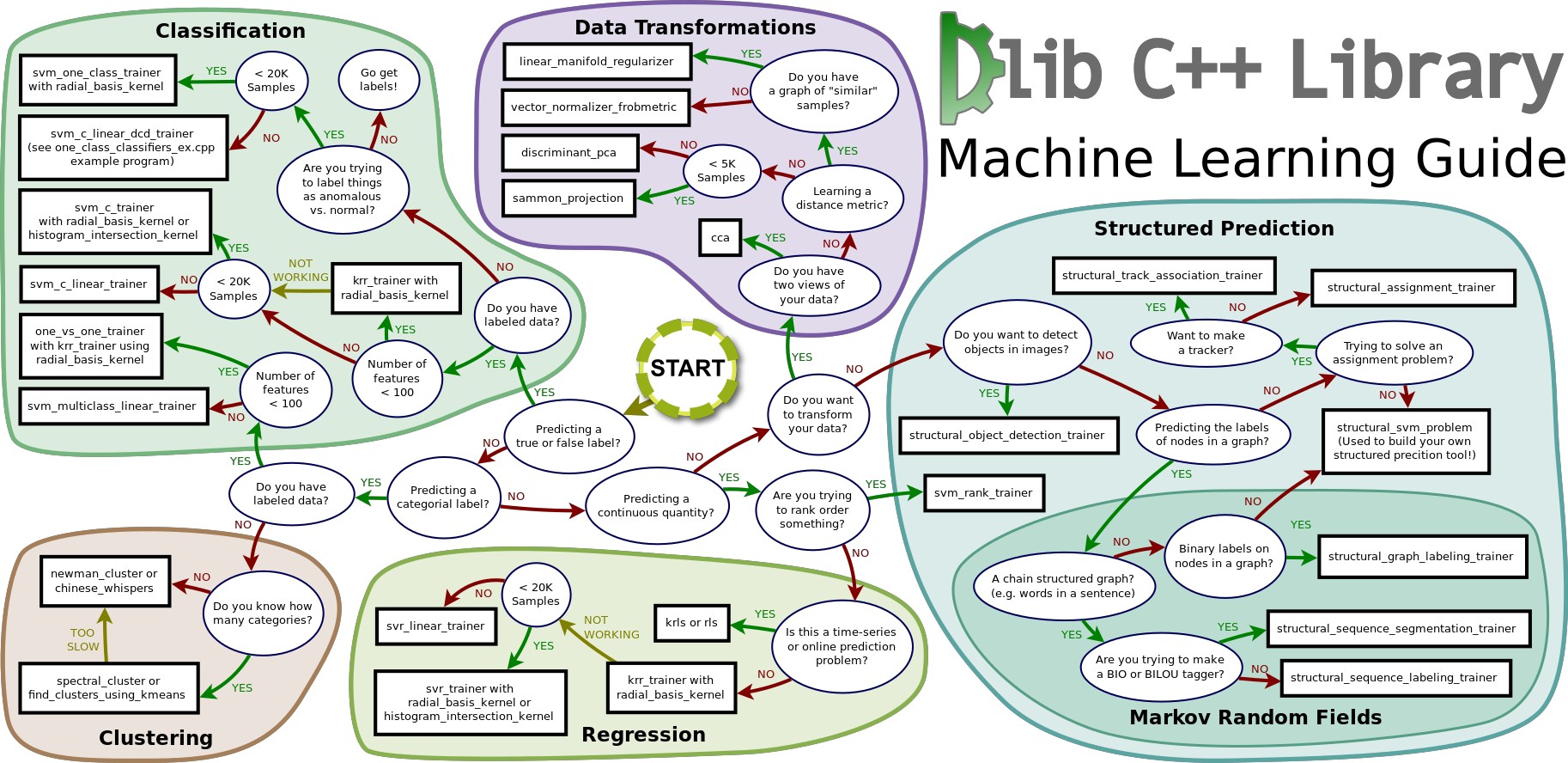
スニペット
簡易的なログ残し
| |
シードの設定
| |
画像の変換
基本はPillow形式だが、numpyやtorchの形式を相互に変換する必要がある。
| |
borderの追加
| |

torchのdatasetの画像確認
| |
Contourの確認スニペット
| |
階層的クラスタリング
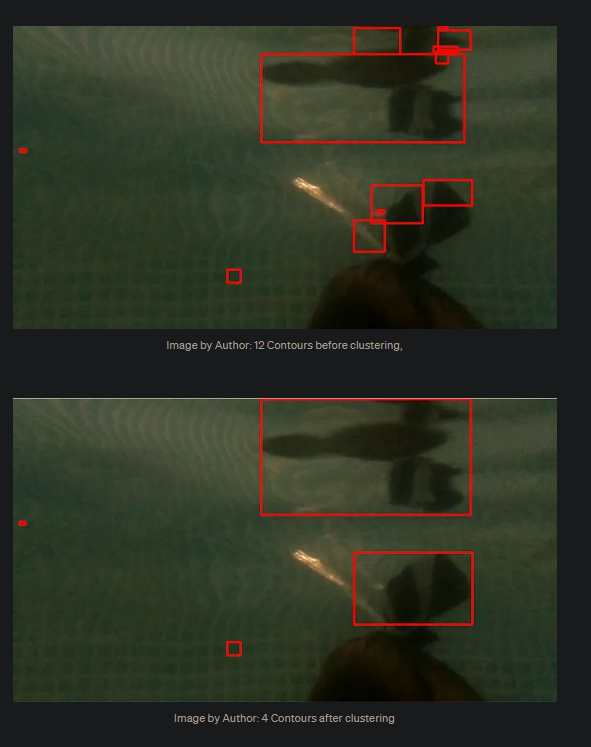
- CVでの階層的クラスタリング(agglomerative clustering algorithm)は、Contourのクラスタリングをする手法
- その際のbboxの距離は、NMSやIoUなどとは違い、距離自体は、サイズを加味して計算する
- 基本的に閾値以下で隣接するモノをまとめる手法
- すべてのcontourについて比較する必要がある為、計算量Oは最低でも$O(n^2)$になるはず
- 実際は一次元だが、イメージはDendrogramで、距離が閾値以下がまとまる
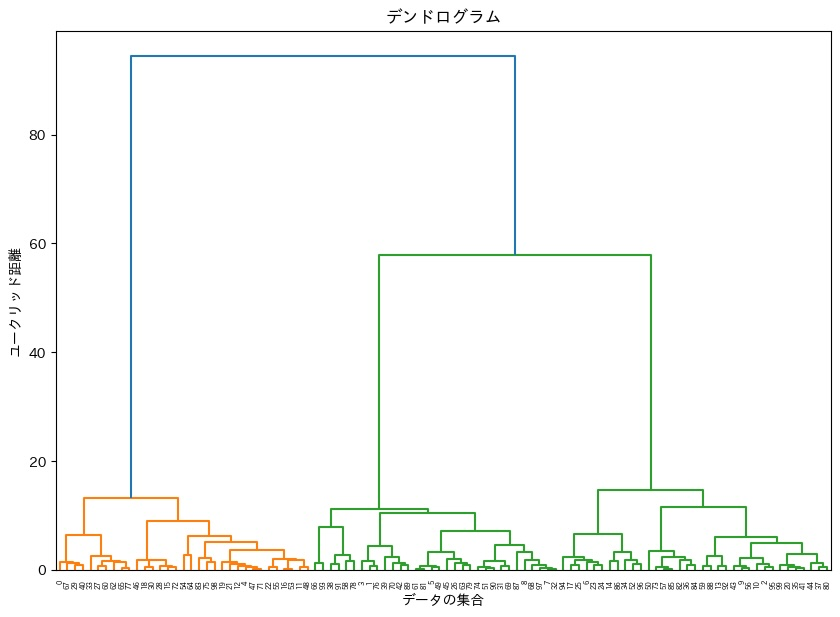
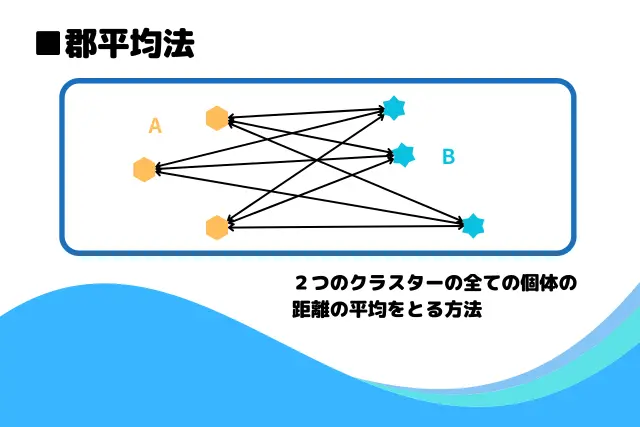
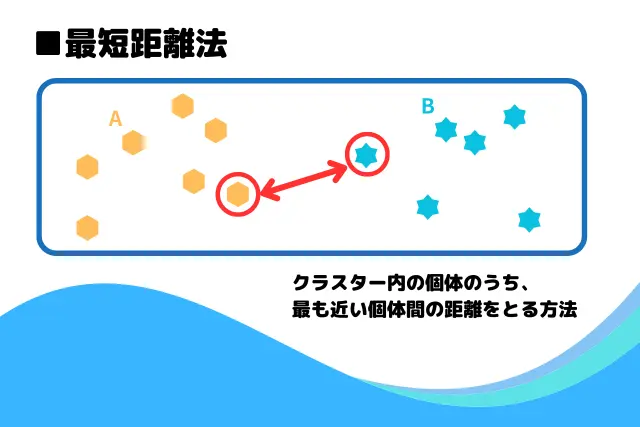
クラスターの結合方法は次の4つがあるが、このアルゴは3番の最短距離法を利用している。
- ウォード法:クラスターの併合時、平方和が最小になるようにする方法
- 最長距離法:距離の最も遠いデータ同士から併合していくする方法
- 最短距離法:距離の最も近いデータ同士から併合していく方法
- 群平均法:すべてのデータの平均を計算し、クラスターの距離として併合する方法
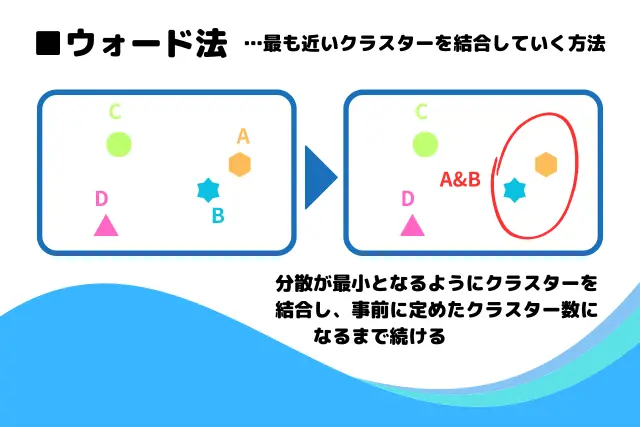

| |
結果
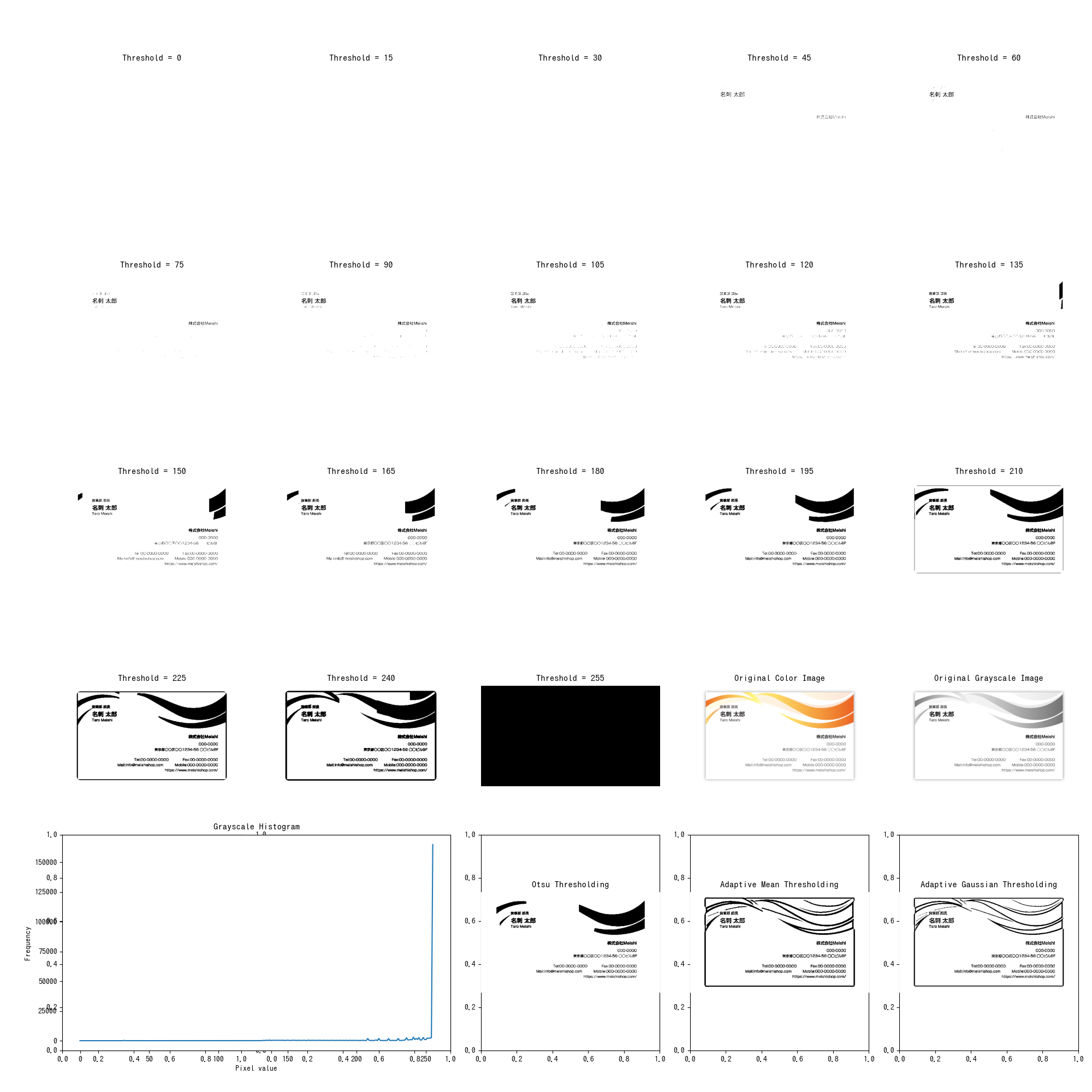
二値化の確認
二値化は必須スキルなので、一覧にして確認する為のスニペット。
| |
元画像

結果
まとめ
- CV周りは理解しなければならない事が多い
- 上記の通り、古典的なCVのアルゴでも、手法も多岐に渡る
- Deep learning, ViTとCVの最新技術はまだまだ続く
参考文献
- #007 OpenCV projects - Image segmentation with Watershed algorithm
- Non-local means - Wikipedia
- How can I sharpen an image in OpenCV? - Stack Overflow
- Unsharp masking - Wikipedia
- アンシャープマスキング | 天文学辞典
- python - Deblurring an image in order to perform edge detection - Stack Overflow
- image - Finding a tight contour around a blurry object with Python OpenCV - Stack Overflow
- Saliency Mapを使って画像を良い感じに切り抜くAIを作った #Python - Qiita
- Sharpening An Image using OpenCV Library in Python
- python+OpenCVでエッジを保存した平滑化(BilateralFilter, NLMeansFilter) #Python - Qiita
- Image-Py/sknw: build net work from skeleton image (2D-3D)
- [scikit-image] 23. 画像の細線化(morphology.skeletonize) – サボテンパイソン
- 画像位置合わせ:SIFTから深層学習まで #Python - Qiita
- アンチエイリアスとは?
- 画像認識の初歩、SIFT,SURF特徴量 | PPT
- 関西CVPRML勉強会(特定物体認識) 2012.1.14
- computer vision - What is a feature descriptor in image processing (algorithm or description)? - Stack Overflow
- 画像認識の初歩、SIFT,SURF特徴量 | PPT
- Feature Matching using Brute Force in OpenCV - GeeksforGeeks
- BRISK(Binary Robust Invariant Scalable Keypoints) - ComputerVisionまとめの部屋
- Feature Matching using Brute Force in OpenCV - GeeksforGeeks
- Feature Matching — OpenCV-Python Tutorials beta documentation
- OpenCV: Feature Matching
- Fixed-radius near neighbors - Wikipedia
- https://chrisalbon.com/code/machine_learning/nearest_neighbors/radius_based_nearest_neighbor_classifier/
- Fast Approximate Nearest Neighbor Search — opencv 2.2 (r4295) documentation
- OpenCV - cv2.distanceTransform で距離変換を行う方法 - pystyle
- Pタイル法 | イメージングソリューション
- 【可視化】カルバックライブラーなど分布の差を表す指標の違い - プロクラシスト
- 物体セグメンテーションアルゴリズム"watershed"を詳しく #OpenCV - Qiita
- 画像情報処理 実習資料
- 幾何学的変換 - Wikipedia
- python - OpenCV - Blob/ Defect/ Anomaly Detection - Stack Overflow
- outliers - Why isn’t RANSAC most widely used in statistics? - Cross Validated
- RANSAC Circle
- 特徴抽出・ブロブ解析 株式会社ガゾウ
- 図形の輪郭座標と面積から円形度を計算する · kamatari
- image processing - OpenCV circle distortion detection - Stack Overflow
- Huモーメント不変量による類似画像検索 -
- Image moment - Wikipedia
- Huモーメント不変量による類似画像検索 -
- Huモーメントって何? #OpenCV - Qiita
- 画像のモーメントについての備忘録 - plant-raspberrypi3のブログ
- 領域(輪郭)の特徴 — OpenCV-Python Tutorials 1 documentation
- 【OpenCV-Python】findContoursによる輪郭検出 | イメージングソリューション
- Hough変換による3次元空間上の直線検出の方法 | DATUM STUDIO株式会社
- ハフ変換 (Hough Transform) による直線・円の検出 | CVMLエキスパートガイド
- 【画像処理】PythonでOpenCVを使った色空間の変換 #Python - Qiita
- エッジ検出を完全理解!主要3フィルタとCanny法の実装手順を解説 - DS Media by Tech Teacher
- OpenCV & Python - Canny Edge Detection - Meccanismo Complesso
- コンピュータビジョンのセカイ - 今そこにあるミライ(40) iPhoneアプリ「漫画カメラ」で使われている画像処理手法その1 | TECH+(テックプラス)
- OpenCVにおけるラプラシアンフィルタとアパーチャサイズ - たくのろじぃのメモ部屋
- Difference of Gaussians Edge Enhancement Algorithm - Java Tutorial | Olympus LS
- Canny法によるエッジ検出 — OpenCV-Python Tutorials 1 documentation
- エッジ検出を完全理解!主要3フィルタとCanny法の実装手順を解説 - DS Media by Tech Teacher
- cs.toronto.edu/~guerzhoy/320/lec/edgedetection.pdf
- コンピュータビジョンのセカイ - 今そこにあるミライ(40) iPhoneアプリ「漫画カメラ」で使われている画像処理手法その1 | TECH+(テックプラス)
- The relationship between the world coordinate system and the camera… | Download Scientific Diagram
- Agglomerative Clustering for OpenCV Contours with Python | by Cullen Sun | Medium
- aleju/imgaug: Image augmentation for machine learning experiments.
- このデータセットにはどの距離を用いればよいの??~ユークリッド距離・マンハッタン距離・チェビシェフ距離・マハラノビス距離~ | データ化学工学研究室(金子研究室)@明治大学 理工学部 応用化学科
- 階層クラスター分析とは?非階層クラスター分析との違いについても解説 - エリマケ!
- 配列の編集距離(ハミング距離,レーベンシュタイン距離) | ふかひれぐらたん研究所
